Vieri's POV: September 2020

Shalom

Om Swastiastu

Namo Buddhaya

Rahayu

Salam Kebajikan

Salam Sejahtera Untuk Seluruh Alam

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

ﺇِﻥَّ ﺍﻟْﺤَﻤْﺪَ ﻟِﻠَّﻪِ ﻧَﺤْﻤَﺪُﻩُ ﻭَﻧَﺴْﺘَﻌِﻴْﻨُﻪُ ﻭَﻧَﺴْﺘَﻐْﻔِﺮُﻩْ ﻭَﻧَﻌُﻮﺫُ ﺑِﺎﻟﻠﻪِ ﻣِﻦْ ﺷُﺮُﻭْﺭِ ﺃَﻧْﻔُﺴِﻨَﺎ ﻭَﻣِﻦْ ﺳَﻴِّﺌَﺎﺕِ ﺃَﻋْﻤَﺎﻟِﻨَﺎ، ﻣَﻦْ ﻳَﻬْﺪِﻩِ ﺍﻟﻠﻪُ ﻓَﻼَ ﻣُﻀِﻞَّ ﻟَﻪُ ﻭَﻣَﻦْ ﻳُﻀْﻠِﻞْ ﻓَﻼَ ﻫَﺎﺩِﻱَ ﻟَﻪُ. ﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻻَ ﺇِﻟَﻪَ ﺇِﻻَّ ﺍﻟﻠﻪ ﻭَﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻣُﺤَﻤَّﺪًﺍ ﻋَﺒْﺪُﻩُ ﻭَﺭَﺳُﻮْﻟُﻪُ.

Saya akan memperkenalkan diri. Saya Paisal Vieri Eka Tama Simbolon (27) murid kelas XI IPS 2 di Sekolah Menengah Atas Negeri 63 Jakarta. Dan saya suka perubahan. Follow instagram @paisalts_.

LANGSUNG YAKK...................

Contoh Soal 1 :

Persamaan bayangan kurva y = x² – 2x – 3 oleh rotasi [0, 180°], kemudian dilanjutkan oleh pencerminan terhadap garis y = -x adalah ….

A. y = x² – 2x – 3

B. y = x² – 2x + 3

C. y = x² + 2x + 3

D. x = y² – 2y – 3

E. x = y² + 2y + 3

Jawaban : D

Pembahasan :

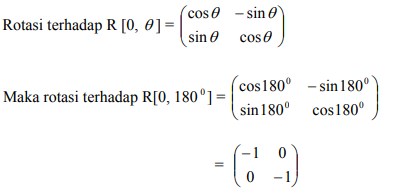
soal transformasi geometri dan jawaban no 2

Rotasi sudut-sudut yang lain dapat dihitung sendiri menggunakan kaidah trigonometri.

pencerminan terhadap garis y = -x

soal transformasi geometri dan jawaban no 2-1

Contoh Soal 2 :

Persamaan bayangan dari lingkaran x² +y² +4x – 6y – 3 = 0 oleh transformasi yang berkaitan dengan matriks

adalah….

A. x² + y² – 6x – 4y- 3 = 0

B. X² + y² – 6x + 4y- 3 = 0

C. x² + y² + 6x – 4y- 3 = 0

D. x² + y² – 4x + 6y- 3 = 0

E. x² + y² + 4x – 6y+ 3 = 0

Jawaban : A

Pembahasan :

Contoh Soal 3 :

Persamaan bayangan kurva y = 3x² + 2x − 1 oleh pencerminan terhadap sumbu X dilanjutkan dengan pencerminan terhadap sumbu Y adalah ... (UN 2016)
A. y = −3x² − 2x − 1
B. y = −3x² + 2x + 1
C. y = −3x² + 2x − 1
D. y = 3x² + 2x + 1
E. y = 3x² − 2x + 1

Jawaban : B

Pembahasan :
Misalkan :
T₁ = matriks yang bersesuaian dengan pencerminan terhadap sumbu X.
T₂ = matriks yang bersesuaian dengan pencerminan terhadap sumbu Y.
T = T₂ o T₁

dan Bayangan titik (x, y) oleh transformasi T adalah :
Dari persamaan matriks diatas, diperoleh :
x' = -x ↔ x = -x'
y' = -y ↔ y = -y'

Substitusi x dan y ke persamaan kurva :
y = 3x² + 2x − 1
⇒ (-y') = 3(-x')² + 2(-x') − 1
⇔ -y' = 3(x')² − 2x' − 1
⇔ y' = −3(x')² + 2x' + 1

Jadi, persamaan bayangan kurva adalah :
y = −3x² + 2x + 1

Contoh Soal 4 :

Persamaan peta garis 3x – 4y = 12, karena refleksi terhadap garis y – x = 0, dilanjutkan oleh transformasi yang bersesuaian dengan matriks $\left(\begin{array}{rr} -3&5\\ -1&1\end{array}\right)$ adalah… (UAN ’03)

Pembahasan 1:

Diketahui matriksnya:

Rotasi = $\left(\begin{array}{rr} 0&1\\ 1&0\end{array}\right)$

Transformasi = $\left(\begin{array}{rr} -3&5\\ -1&1\end{array}\right)$

Persamaan garis direfleksi kemudian ditransformasi adalah:

$\left(\begin{array}{r} x'\\ y'\end{array}\right) = \left(\begin{array}{rr} -3&5\\ -1&1\end{array}\right) \left(\begin{array}{rr} 0&1\\ 1&0\end{array}\right) \left(\begin{array}{r} x\\ y\end{array}\right) = \left(\begin{array}{rr} 5&-3\\ 1&-1\end{array}\right) \left(\begin{array}{r} x'\\ y'\end{array}\right)$

$\left(\begin{array}{r} x\\ y\end{array}\right) = - \frac{1}{2} \left(\begin{array}{rr} -1&3 \\ -1&5\end{array} \right) \left(\begin{array}{r} x'\\ y'\end{array}\right) = \begin{pmatrix} \frac{x'-3y'}{2} \\ \frac{x'-5y'}{2} \end{pmatrix}$

Kemudian disubstitusikan:

$3x - 4y = 12 \overset{substitusi}{\rightarrow}3 (\frac{x'- 3y'}{2}) - 4(\frac{x'-5y'}{2}) = 12$

$3(x' - 3y') - 4(x'- 5y') = 24$

$3x' - 9y' - 4x' + 20y' =24$

$-x' + 11y' =24$

Hasilnya:

$11y - x =24$

Contoh Soal 5 :

Pencerminan terhadap sumbu x adalah A, pencerminan terhadap sumbu y adalah B dan rotasi 180^o terhadap puasat O adalah H. Tentukan matriks B(A(HA)). (UMPTN ’90)

Pembahasan 2:

Diketahui:

Pencerminan terhadap sumbu $x,A = \left(\begin{array}{rr} 1&0\\ 0&-1\end{array}\right)$
Pencerminan terhadap sumbu $y,B = \left(\begin{array}{rr} -1&0\\ 0&1\end{array}\right)$
Rotasi 180^o, $H = \left(\begin{array}{rr} cos 180 &-sin180 \\ sin 180 & cos 180\end{array}\right) = \left(\begin{array}{rr} -1&0\\ 0&-1\end{array}\right)$

Maka:

$B(A(HA)) = \left(\begin{array}{rr} -1&0\\ 0&1\end{array}\right) ( \left(\begin{array}{rr} 1&0\\ 0&-1\end{array}\right) [ \left(\begin{array}{rr} -1&0\\ 0&-1\end{array}\right) \left(\begin{array}{rr} -1&0\\ 0&-1\end{array}\right) ]))$

$= \left(\begin{array}{rr} -1&0\\ 0&1\end{array}\right) ( \left(\begin{array}{rr} 1&0\\ 0&-1\end{array}\right) \left(\begin{array}{rr} -1&0\\ 0&1\end{array}\right) )$

$= \left(\begin{array}{rr} -1&0 \\ 0&1\end{array}\right) \left(\begin{array}{rr} -1&0\\ 0&-1\end{array}\right)$

$= \left(\begin{array}{rr} 1&0\\ 0&-1\end{array}\right)$

Contoh Soal 6 :

Oleh matriks $A = \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right)$ , titik $P(1, 2)$ dan titik Q masing-masing ditransformasikan ke titik $P'(2, 3)$ dan $Q'(2,0)$ . Tentukan koordinat titik Q. (SPMB’04)

Pembahasan 3:

Mencari nilai a dari transformasi P:

$\left(\begin{array}{r} x'\\ y'\end{array}\right)= \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right) \left(\begin{array}{r} x\\ y\end{array}\right)\overset{sehingga}{\rightarrow}\left(\begin{array}{r} 2\\ 3\end{array}\right) = \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right) \left(\begin{array}{r} 1\\ 2\end{array}\right)\overset{menjadi}{\rightarrow}\left(\begin{array}{r} 2\\ 3\end{array}\right) = \left(\begin{array}{rr} 2 + 3a\\ 3 + 2a\end{array}\right)$

$a = 0$

Sehingga matriksnya:

$A = \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right) = \left(\begin{array}{rr} 2&0\\ 1&1\end{array}\right)$

Mencari titik Q:

$\left(\begin{array}{r} x'\\ y'\end{array}\right) = \left(\begin{array}{rr} 2&0\\ 1&1\end{array}\right) \left(\begin{array}{r} x\\ y\end{array}\right) \overset{sehingga}{\rightarrow} \left(\begin{array}{r} x\\ y\end{array}\right) = \frac{1}{2} \left(\begin{array}{rr} 1&0\\ -1&2\end{array}\right) \left(\begin{array}{r} x'\\ y'\end{array}\right) \overset{disubstitusi} = {\rightarrow} \left(\begin{array}{r} x\\ y\end{array}\right) = \frac{1}{2} \left(\begin{array}{rr} 1&0\\ -1&2\end{array}\right) \left(\begin{array}{r} 2\\0\end{array}\right)$

$\left(\begin{array}{r} x\\ y\end{array}\right) = \left(\begin{array}{r} 1\\ -1\end{array}\right)$

Sehingga:

$Q(1, -1)$

Contoh Soal 7 :

Dilatasi yang berpusat di titik (3, 1) dengan faktor skala 3, memetakan titik (5, b) ke titik (a, 10). Maka nilai a – b adalah ….
A. 15
B. 11
C. 5
D. 4
E. 2

Pembahasan:

Dilatasi dengan pusat (3, 1) dengan faktor skala 3 akan menghasilkan matriks transformasi berikut.

$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 5 - 3 \\ b- 1 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 2 \\ b- 1 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 6 \\ 3b - 3 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 9 \\ 3b - 2 \end{pmatrix}$

Sehingga dapat diperoleh nilai a dan b:

a = 9
3b – 2 = 10
3b = 12
b = 12 : 3 = 4

Jadi, nilai a – b = 9 – 4 = 5

Jawaban: C

Oke, jadi sekarang kita sudah menguasai Soal Transportasi Translasi, Refleksi, Rotasi, Dilatasi dengan Matriks. Semoga apa yang pelajari hari memberikan manfaat dikemudian hari dan diberkati tuhan yang maha esa.
Wassalamualaikum Warahmatullahi Wabarakatuh
Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam

DAFTAR PUSTAKA

Rumus pada Transformasi Geometri (Translasi, Refleksi, Rotasi, dan Dilatasi ). (2017, November 22). Retrieved September 28, 2020, from idschool.net: https://idschool.net/sma/rumus-pada-transformasi-geometri-translasi-refleksi-rotasi-dan-dilatasi/

Admin. (n.d.). Transformasi Geometri. Retrieved September 28, 2020, from www.studiobelajar.com: https://www.studiobelajar.com/transformasi-geometri/

Ilham, A. (2020, Mei 17). Contoh Soal Transformasi Geometri (Translasi, Refleksi, Rotasi, Dilatasi). Retrieved September 28, 2020, from soalkimia.com: https://soalkimia.com/contoh-soal-transformasi-geometri/

Maker, Z. (2017, April 6). Pembahasan Soal UN Transformasi. Retrieved September 28, 2020, from smatika.blogspot.com: https://smatika.blogspot.com/2017/04/pembahasan-soal-ujian-nasional.html

Vieri's POV

Senin, 28 September 2020

Soal Transformasi Translasi, Refleksi, Rotasi, Dilatasi dengan Matriks

Jakarta dan Hidup Layak

Cari Blog Ini