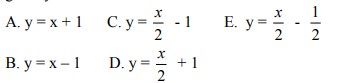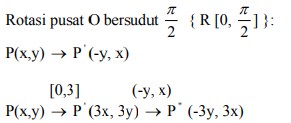KOMPOSISI 2, 3, 4 TRANSFORMASI (GABUNGAN TRANSLASI, REFLEKSI, ROTASI, DILATASI) 1 BALOK

PAISAL VIERI EKA TAMA SIMBOLON (28) XI IPS 2

Shalom

Om Swastiastu 

Namo Buddhaya 

Rahayu 

Salam Kebajikan 

Salam Sejahtera Untuk Seluruh Alam

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

ﺇِﻥَّ ﺍﻟْﺤَﻤْﺪَ ﻟِﻠَّﻪِ ﻧَﺤْﻤَﺪُﻩُ ﻭَﻧَﺴْﺘَﻌِﻴْﻨُﻪُ ﻭَﻧَﺴْﺘَﻐْﻔِﺮُﻩْ ﻭَﻧَﻌُﻮﺫُ ﺑِﺎﻟﻠﻪِ ﻣِﻦْ ﺷُﺮُﻭْﺭِ ﺃَﻧْﻔُﺴِﻨَﺎ ﻭَﻣِﻦْ ﺳَﻴِّﺌَﺎﺕِ ﺃَﻋْﻤَﺎﻟِﻨَﺎ، ﻣَﻦْ ﻳَﻬْﺪِﻩِ ﺍﻟﻠﻪُ ﻓَﻼَ ﻣُﻀِﻞَّ ﻟَﻪُ ﻭَﻣَﻦْ ﻳُﻀْﻠِﻞْ ﻓَﻼَ ﻫَﺎﺩِﻱَ ﻟَﻪُ. ﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻻَ ﺇِﻟَﻪَ ﺇِﻻَّ ﺍﻟﻠﻪ ﻭَﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻣُﺤَﻤَّﺪًﺍ ﻋَﺒْﺪُﻩُ ﻭَﺭَﺳُﻮْﻟُﻪُ.

Saya akan memperkenalkan diri. Saya Paisal Vieri Eka Tama Simbolon (28) murid kelas XI IPS 2 di Sekolah Menengah Atas Negeri 63 Jakarta.

 

LANGSUNG YAKK...................

KOMPOSISI 2, 3, 4 TRANSFORMASI (GABUNGAN TRANSLASI, REFLEKSI, ROTASI, DILATASI) 1 BALOK YG TITIK KOORDINATNYA A(2,2), B(5,2), C(5,4), D(2,4), E(4,3), F(7,3), G(7,5), H(4,5) Dan perhitungan dengan perhitungan biasa dan perhitungan matriks

 

Terima kasih kepada Ibu DR Lizza Novrida, semoga apa yang pelajari hari memberikan manfaat dikemudian hari dan diberkahi tuhan yang maha esa.
Wassalamualaikum Warahmatullahi Wabarakatuh

Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam  

Transformasi : Translasi, Dilatasi, Refleksi dan Rotasi 1 Titik, 1 Garis, 1 Persegi Panjang, dan 1 Kubus

PAISAL VIERI EKA TAMA SIMBOLON (27) XI IPS 2

Shalom

Om Swastiastu 

Namo Buddhaya 

Rahayu 

Salam Kebajikan 

Salam Sejahtera Untuk Seluruh Alam

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

ﺇِﻥَّ ﺍﻟْﺤَﻤْﺪَ ﻟِﻠَّﻪِ ﻧَﺤْﻤَﺪُﻩُ ﻭَﻧَﺴْﺘَﻌِﻴْﻨُﻪُ ﻭَﻧَﺴْﺘَﻐْﻔِﺮُﻩْ ﻭَﻧَﻌُﻮﺫُ ﺑِﺎﻟﻠﻪِ ﻣِﻦْ ﺷُﺮُﻭْﺭِ ﺃَﻧْﻔُﺴِﻨَﺎ ﻭَﻣِﻦْ ﺳَﻴِّﺌَﺎﺕِ ﺃَﻋْﻤَﺎﻟِﻨَﺎ، ﻣَﻦْ ﻳَﻬْﺪِﻩِ ﺍﻟﻠﻪُ ﻓَﻼَ ﻣُﻀِﻞَّ ﻟَﻪُ ﻭَﻣَﻦْ ﻳُﻀْﻠِﻞْ ﻓَﻼَ ﻫَﺎﺩِﻱَ ﻟَﻪُ. ﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻻَ ﺇِﻟَﻪَ ﺇِﻻَّ ﺍﻟﻠﻪ ﻭَﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻣُﺤَﻤَّﺪًﺍ ﻋَﺒْﺪُﻩُ ﻭَﺭَﺳُﻮْﻟُﻪُ.

Saya akan memperkenalkan diri. Saya Paisal Vieri Eka Tama Simbolon (27) murid kelas XI IPS 2 di Sekolah Menengah Atas Negeri 63 Jakarta. Dan saya suka perubahan. Follow instagram @paisalts_.

 

LANGSUNG YAKK...................

 

TRANFORMASI TITIK

Refleksi

Bayangan titik $A$ dengan $A(-1,4)$ jika direfleksikan terhadap garis $y=-x$ adalah $\cdots \cdot$
A. $A^{\prime }(4,1)$                      D. $A^{\prime }(4,3)$
B. $A^{\prime }(-4,1)$                    E. $A^{\prime }(-4,-1)$
C. $A^{\prime }(4,-1)$

Pembahasan :

Apabila titik $A(x,y)$

direfleksikan terhadap garis $y=-x$, maka bayangan titik $A$ adalah $A^{\prime }=(-y,-x)$. 
Jadi, bayangan titik $A(-1,4)$ adalah $A^{\prime }(-4,1)$.
(Jawaban B)

Dilatasi

Diketahui koordinat titik $P(-8,12)$. Dilatasi $[P,1]$ memetakan titik $(-4,8)$ ke titik $\cdots \cdot$
A. $(-4,8)$                  D. $(4,-16)$
B. $(-4,16)$                E. $(4,-8)$
C. $(-4,-8)$

Pembahasan

Konsep dilatasi: Jika titik $(x,y)$

didilatasikan dengan pusat $(a,b)$ dan faktor skala $k$, maka bayangan titiknya berada di koordinat $\left(k\right(x-a)+a,k(y-b)+b)$.
Bayangan titik $(-4,8))$ setelah didilatasikan dengan pusat $(-8,12)$ dan faktor skala $1$ adalah
$\left(1\right(-4-(-8))+(-8),1(8-12)+12)$ $=(-4,8)$ 
Dilatasi $[P,1]$ memetakan titik $(-4,8)$ ke titik $(-4,8)$
(Jawaban A)

 

Translasi

Diketahui koordinat titik P adalah (4,-1). Oleh karena translasi (2a) diperoleh bayangan titik P yaitu P'(-2a, -4). Tentukanlah nilai a.

Pembahasan:

T = (2a) : P(4,-1) → P'(-2a , -4)  

P'(-2a, -4) = P'(2+4, a+(-1))

P'(-2a, -4) = P'(6, (a-1))

⟺-2a = 6

⟺ a = 6/-2

⟺ a = -3

Jadi, nilai a adalah -3

 

Rotasi

Tentukan bayangan titik (-2, 8) oleh  rotasi R(O, 135)!

a.       (-3√2, -5√2)

b.      (3√2, 5√2)

c.       (-3√2,-5√2)

d.      (3√2, 5√2)

e.       (-3√2, 5√2)

Pembahasan :

TRANFORMASI GARIS

Refleksi

Contoh Soal 1

Bayangan garis y = 2x + 2 yang dicerminkan terhadap garis y= x adalah. . .

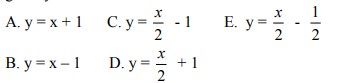
Jawaban : C

Pembahasan : 

Conoth Soal 2

Bayangan garis y = 2x + 2 yang dicerminkan terhadap garis y= x adalah. . .

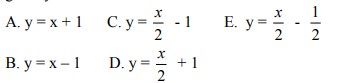
Jawaban : C

Pembahasan : 

Dilatasi

Tentukan bayangan garis 3x + 4y – 5 = 0 oleh dilatasi dengan pusat (-2, 1) dan faktor skala 2!

A. 3x + 4y + 12 = 0

B. 3x + 4y – 12 = 0

C. 3x – 4y + 12 = 0

D. -3x + 4y + 12 = 0

E. 3x – 4y – 12 = 0

Pembahasan :

Translasi

Tentukan bayangan garis y = 3x – 5 oleh translasi T (-2, 1)! 

a.       y = 2x + 2 

b.      y = 2x - 2 

c.       y = 3x + 2 

d.      y = 3x - 2 

e.       y = 2x + 3 

Pembahasan :

Rotasi

Sebuah garis 2x – 3y – 4 = 0 dirotasikan sebesar 180^o dengan titik pusat rotasi (1,-1). Tentukan persamaan garis setelah dirotasikan!
Jawab:
Misalkan titik A(x,y) adalah sembarang titik pada garis tersebut, sehingga

Langkah-langkah rotasinya sebagai berikut.

1. Translasikan titik A(x,y) dengan T, sehingga diperoleh

   

2. Rotasikan (x-1,y+1) sebesar 180^o dan pusat O(0,0), diperoleh

   

3. Translasikan kembali koordinat (-x+1,-y-1) dengan T, diperoleh

   

Sehingga

Jadi x’ = –x+2, dan y’= –y – 2 atau x = –x’+2, dan y= –y’ – 2, sehingga persamaan garis setelah dirotasikan adalah
2(-x+2) – 3(-y-2) – 4 = 0
-2x + 3y + 6 = 0

TRANFORMASI PERSEGI PANJANG

Contoh Soal 1

Luas bayangan persegipanjang PQRS dengan

P(-1,2), Q(3,2), R (3,-1), S(-1,-1)

karena dilatasi [0,3] dilanjutkan rotasi pusat O bersudut π/2 adalah…

A. 36

B. 48

C.72

D. 96

E. 108

Jawaban : E

Pembahasan : 

dilatasi [0,3] :

[O,3k] : P(x,y) → P ‘(3x, 3y)

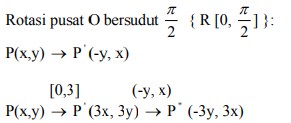
Sehingga :

P(x,y) → P” (-3y, 3x)

P(-1,2), Q(3,2), R (3,-1), S(-1,-1)

P(-1,2) → P” (-6,-3)

Q(3,2) → Q” (-6,9)

R (3,-1) → R” (3,9)

S(-1,-1) → S” (3,-3)

Buat sketsa gambarnya:

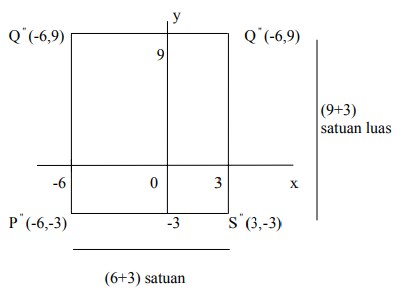
Sehingga luas transformasinya adalah :

Panjang (p) x lebar (l) = 12 x 9 = 108 satuan luas

Contoh Soal 2

Diketahui persegi panjang ABCD, dengan A(0,0), B(4,0), C(4,3) dan D(0,3). Tentukan bayangan dari persegi panjang ABCD tersebut jika di rotasi sebesar 270^o dengan pusat rotasi P(7,3)!
Jawab:
Tabel Koordinat titik dan bayangan titik oleh rotasi sejauh 270^o dan pusat (7,3)

Rotasi sejauh 2700 dengan pusat rotasi P(7,3)
Titik Asal	Translasi T	Rotasi 270o Pusat (0,0)	Translasi T (bayangan akhir)
A(0,0)	(-7,-3)	(-3,7)	(-3+7,7+3) =A’(4,10)
B(4,0)	(-3,-3)	(-3,3)	(-3+7,3+3) = B’(4,6)
C(4,3)	(-3.0)	(0,3)	(0+7,3+3) = C’(7,6)
D(0,3)	(-7,0)	(0,7)	(0+7, 7+3) = D’(7,10)

Gambar Grafik.

---

TRANFORMASI KUBUS

Refleksi

Dilatasi

Translasi

Rotasi

 

Terima kasih kepada Ibu DR Lizza Novrida, semoga apa yang pelajari hari memberikan manfaat dikemudian hari dan diberkati tuhan yang maha esa.
Wassalamualaikum Warahmatullahi Wabarakatuh
Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam  

DAFTAR PUSTAKA

Admin. (2016). Rotasi dengan Pusat (a,b). Retrieved Oktober 19, 2020, from m-edukasi.kemdikbud.go.id: https://m-edukasi.kemdikbud.go.id/medukasi/produk-files/kontenkm/km2016/KM201606/materi2.html

Admin. (2018, Juni). Kumpulan Soal dan Pembahasan Translasi (Pergeseran) . Retrieved Oktober 19, 2020, from ilmuku-duniaku14.blogspot.com: http://ilmuku-duniaku14.blogspot.com/2018/06/kumpulan-soal-dan-pembahasan-translasi.html

Admin. (n.d.). Kumpulan Soal Transformasi. Retrieved Oktober 19, 2020, from cintamatematika467.wordpress.com: https://cintamatematika467.wordpress.com/kumpulan-soal-transformasi/

Ilham, A. (2020, Mei 17). Contoh Soal Transformasi Geometri (Translasi, Refleksi, Rotasi, Dilatasi). Retrieved Oktober 19, 2020, from soalkimia.com: https://soalkimia.com/contoh-soal-transformasi-geometri/

Sukardi. (2019, April 30). Soal dan Pembahasan Super Lengkap – Transformasi Geometri. Retrieved Oktober 19, 2020, from mathcyber1997.com: https://mathcyber1997.com/soal-dan-pembahasan-transformasi-geometri-tingkat-sma/

Unknown. (2016, Juni 9). Soal Transformasi (Translasi, Refleksi, Rotasi, dan Dilatasi) Kelas XI dan Pembahasan. Retrieved Oktober 19, 2020, from defajhareborn.blogspot.com: http://defajhareborn.blogspot.com/2015/06/soal-transformasi-translasi-refleksi.html