NILAI STASIONER, FUNGSI NAIK DAN FUNGSI TURUN

NILAI STASIONER, FUNGSI NAIK DAN FUNGSI TURUN

Paisal Vieri Eka Tama Simbolon (28) XI IPS 2

Shalom

Om Swastiastu 

Namo Buddhaya 

Rahayu 

Salam Kebajikan 

Salam Sejahtera Untuk Seluruh Alam

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

ﺇِﻥَّ ﺍﻟْﺤَﻤْﺪَ ﻟِﻠَّﻪِ ﻧَﺤْﻤَﺪُﻩُ ﻭَﻧَﺴْﺘَﻌِﻴْﻨُﻪُ ﻭَﻧَﺴْﺘَﻐْﻔِﺮُﻩْ ﻭَﻧَﻌُﻮﺫُ ﺑِﺎﻟﻠﻪِ ﻣِﻦْ ﺷُﺮُﻭْﺭِ ﺃَﻧْﻔُﺴِﻨَﺎ ﻭَﻣِﻦْ ﺳَﻴِّﺌَﺎﺕِ ﺃَﻋْﻤَﺎﻟِﻨَﺎ، ﻣَﻦْ ﻳَﻬْﺪِﻩِ ﺍﻟﻠﻪُ ﻓَﻼَ ﻣُﻀِﻞَّ ﻟَﻪُ ﻭَﻣَﻦْ ﻳُﻀْﻠِﻞْ ﻓَﻼَ ﻫَﺎﺩِﻱَ ﻟَﻪُ. ﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻻَ ﺇِﻟَﻪَ ﺇِﻻَّ ﺍﻟﻠﻪ ﻭَﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻣُﺤَﻤَّﺪًﺍ ﻋَﺒْﺪُﻩُ ﻭَﺭَﺳُﻮْﻟُﻪُ.

Saya akan memperkenalkan diri. Saya Paisal Vieri Eka Tama Simbolon (28) murid kelas XI IPS 2 di Sekolah Menengah Atas Negeri 63 Jakarta. 

 

Tegalwangi

Source : GNFI

 

LANGSUNG YAKK..................

Diposkan pada April 8, 2020 oleh Sukardi, S.Pd

Materi, Soal, dan Pembahasan – Fungsi Naik dan Fungsi Turun

Fungsi naik, fungsi turun, dan fungsi diam (stasioner) merupakan kondisi dari turunan pertama suatu fungsi pada suatu interval tertentu. Kondisi yang dimaksud dapat berupa berikut.

1. Jika $f^{\prime }\left(x\right)$

bertanda positif, atau $f^{\prime }\left(x\right)>0$ bertanda negatif, atau $f^{\prime }\left(x\right)<0$ bertanda netral, atau $f^{\prime }\left(x\right)=0$

3. , maka kurva fungsi dalam keadaan tidak turun dan tidak naik, istilahnya kita sebut sebagai stasioner (disebut juga fungsi diam).

 

Baca Juga: Soal dan Pembahasan – Turunan Fungsi Menggunakan Limit

Kondisi suatu fungsi $y=f\left(x\right)$

dalam keadaan naik, turun, atau diam
Diberikan fungsi $y=f\left(x\right)$ dalam interval $I$ dengan $f\left(x\right)$ diferensiabel (dapat diturunkan) pada setiap $x$ di dalam interval $I$

.

1. Jika $f^{\prime }\left(x\right)>0$

, maka kurva $f\left(x\right)$ akan selalu naik pada interval $I$ , maka kurva $f\left(x\right)$ akan selalu turun pada interval $I$ , maka kurva $f\left(x\right)$ stasioner (tetap/diam) pada interval $I$ , maka kurva $f\left(x\right)$ tidak pernah turun pada interval $I$ , maka kurva $f\left(x\right)$ tidak pernah naik pada interval $I$

5. .

Perhatikan sketsa grafik suatu fungsi $f\left(x\right)$

berikut.

Perhatikan bahwa kurva yang ditandai dengan warna merah adalah ketika fungsi itu dikatakan naik, dan biru untuk fungsi turun. Titik $a$ dan $b$ disebut titik stasioner, yaitu titik di mana fungsi itu diam (tidak naik maupun tidak turun). Fungsi $f\left(x\right)$ naik saat $x<a$ atau $x>b$, sedangkan $f\left(x\right)$ turun pada saat $a<x<b$.

, maka kurva fungsi dalam keadaan naik (disebut fungsi naik).

Jika $f^{\prime }\left(x\right)$

, maka kurva fungsi dalam keadaan turun (disebut fungsi turun).

Jika $f^{\prime }\left(x\right)$

.

Jika $f^{\prime }\left(x\right)<0$

.

Jika $f^{\prime }\left(x\right)=0$

.

Jika $f^{\prime }\left(x\right)\ge 0$

.

Jika $f^{\prime }\left(x\right)\le 0$

Contoh Soal 1

Interval $x$ yang membuat kurva fungsi $f\left(x\right)=x^3-6x^2+9x+2$ selalu turun adalah $\cdots \cdot$
A. $-1<x<3$
B. $0<x<3$
C. $1<x<3$
D. $x<1$ atau $x>3$
E. $x<0$ atau $x>3$

Pembahasan

Diketahui $f\left(x\right)=x^3-6x^2+9x+2$

, sehingga turunan pertamanya adalah $f^{\prime }\left(x\right)=3x^2-12x+9$.
Kurva $f\left(x\right)$ selalu turun jika diberi syarat $f^{\prime }\left(x\right)<0$.
$\begin{array}{cc}3x^2-12x+9& <0\\ \text{Kedua ruas dibagi}& \text{dengan}3\\ x^2-4x+3& <0\\ (x-3)(x-1)& <0\\ \therefore 1<x& <3\end{array}$
Jadi, interval $x$ yang membuat kurva fungsi $f\left(x\right)$ selalu turun adalah $1<x<3$

(Jawaban C)

Contoh Soal 2

Diberikan fungsi $g\left(x\right)=2x^3-9x^2+12x$. Interval $x$ yang memenuhi kurva fungsi $g\left(x\right)$ selalu naik adalah $\cdots \cdot$
A. $x<-2$ atau $x>-1$
B. $x<-1$ atau $x>2$
C. $x<1$ atau $x>2$
D. $1<x<2$
E. $-1<x<2$

Pembahasan

Diketahui $g\left(x\right)=2x^3-9x^2+12x$

, sehingga turunan pertamanya adalah $g^{\prime }\left(x\right)=6x^2-18x+12$.
Kurva $g\left(x\right)$ selalu naik jika diberi syarat $g^{\prime }\left(x\right)>0$.
$\begin{array}{cc}6x^2-18x+12& >0\\ \text{Kedua ruas dibagi}& \text{dengan}6\\ x^2-3x+2& >0\\ (x-2)(x-1)& >0\\ \therefore x<1\text{atau}x& >2\end{array}$
Jadi, interval $x$ yang membuat kurva fungsi $g\left(x\right)$ selalu naik adalah $x<1\text{atau}x>2$
(Jawaban C)

Contoh Soal 3

Grafik fungsi $p\left(x\right)=x(6-x{)}^2$ tidak pernah turun dalam interval $\cdots \cdot$
A. $x\le -2$ atau $x\ge 6$
B. $x\le 2$ atau $x\ge 6$
C. $x<2$ atau $x\ge 6$
D. $x\le 2$ atau $x>6$
E. $x<2$ atau $x>6$

Pembahasan

Diketahui $p\left(x\right)=x(6-x{)}^2$

. Turunan pertama $p\left(x\right)$ dapat dicari secara manual dengan menjabarkan seperti berikut (pangkatnya masih kecil, sehingga masih sangat memungkinkan untuk dijabarkan).
$\begin{array}{cc}p\left(x\right)& =x(6-x{)}^2\\ & =x(36-12x+x^2)\\ & =36x-12x^2+x^3\\ p^{\prime }\left(x\right)& =36-24x+3x^2\end{array}$
Grafik fungsi $p\left(x\right)$ tidak pernah turun jika diberi syarat $p^{\prime }\left(x\right)\ge 0$.
$\begin{array}{cc}36-24x+3x^2& \ge 0\\ \text{Kedua ruas dibagi}& \text{dengan}3\\ x^2-8x+12& \ge 0\\ (x-2)(x-6)& \ge 0\\ \therefore x\le 2\text{atau}x& \ge 6\end{array}$
Jadi, interval $x$ yang membuat grafik fungsi $p\left(x\right)$ tidak pernah turun adalah $x\le 2\text{atau}x\ge 6$
(Jawaban B)

Contoh Soal 4

Grafik fungsi $\pi \left(x\right)=x^3+3x^2+5$ tidak pernah naik untuk nilai-nilai $\cdots \cdot$
A. $-2\le x\le 0$
B. $-2\le x<0$
C. $-2<x\le 0$
D. $x\le -2$ atau $x\ge 0$
E. $-2<x<0$

Pembahasan

Diketahui $\pi \left(x\right)=x^3+3x^2+5$

, sehingga turunan pertamanya adalah ${\pi }^{\prime }\left(x\right)=3x^2+6x$.
Grafik fungsi $\pi \left(x\right)$ tidak pernah naik jika diberi syarat ${\pi }^{\prime }\left(x\right)\le 0$.
$\begin{array}{cc}3x^2+6x& \le 0\\ \text{Kedua ruas dibagi}& \text{dengan}3\\ x^2+2x& \le 0\\ x(x+2)& \le 0\\ \therefore -2\le x& \le 0\end{array}$
Jadi, interval $x$ yang membuat grafik fungsi $\pi \left(x\right)$ tidak pernah turun adalah $-2\le x\le 0$
(Jawaban A)

Contoh Soal 5

Soal Nomor 5
Diberikan fungsi $R\left(x\right)=x^3-3x^2+3x-2$. Nilai-nilai $x$ dari fungsi tersebut mengakibatkan kurva fungsi $R\left(x\right)$ $\cdots \cdot$

A. tidak pernah naik
B. tidak pernah turun
C. bisa naik, bisa turun
D. selalu turun
E. selalu naik

Pembahasan

Diketahui $R\left(x\right)=x^3-3x^2+3x-2$

.
Turunan pertamanya adalah $R^{\prime }\left(x\right)=3x^2-6x+3$. Selanjutnya, kita akan mencari titik stasioner fungsi tersebut, yakni saat $R^{\prime }\left(x\right)=0$.
$\begin{array}{cc}3x^2-6x+3& =0\\ \text{Kedua ruas dibagi}& \text{dengan}3\\ x^2-2x+1& =0\\ (x-1{)}^2& =0\\ x& =1\end{array}$
Perhatikan bahwa pada ekspresi $(x-1{)}^2$, kita mendapati bahwa nilai darinya tidak mungkin bertanda negatif (ingat bahwa semua bilangan real yang dikuadratkan tidak akan bertanda negatif), sehingga grafik fungsi $R\left(x\right)$

tidak pernah turun, melainkan stasioner (tetap) atau naik, seperti yang tampak pada sketsa gambar berikut.

(Jawaban B)

Contoh Soal 6

Grafik fungsi $f\left(x\right)=a{x}^3+x^2+5$ akan selalu naik dalam interval $0<x<2$. Nilai $a$ adalah $\cdots \cdot$
A. $-3$                     C. $\frac{1}{3}$                 E. $3$
B. $-\frac{1}{3}$                    D. $1$

Pembahasan

Diketahui $f\left(x\right)=a{x}^3+x^2+5$

dan $f\left(x\right)$ selalu naik di $0<x<2$, mengimplikasikan bahwa
$\begin{array}{cccc}(x-0)(x-2)& <0& & \\ x(x-2)& <0& & \\ x^2-2x& <0& & (\cdots 1)\end{array}$
Turunan pertama $f\left(x\right)$ adalah $f^{\prime }\left(x\right)=3a{x}^2+2x$.
Grafik fungsi $f\left(x\right)$ selalu naik jika diberi syarat $f^{\prime }\left(x\right)>0$.
$\begin{array}{cccc}3a{x}^2+2x& >0& & \\ \text{Kedua ruas dikali}& \text{dengan}-1& & \\ -3a{x}^2-2x& <0& & (\cdots 2)\end{array}$
Kaitkan pertidaksamaan $\left(1\right)$ dan $\left(2\right)$.
$\{\begin{array}{cc}{x}^2-2x& <0\\ -3a{x}^2-2x& <0\end{array}$
Diperoleh $-3a=1\Rightarrow a=-\frac{1}{3}$
Jadi, Nilai $a$ yang membuat $f\left(x\right)$ selalu naik pada interval tersebut adalah $-\frac{1}{3}$ 
(Jawaban B)

Contoh Soal 7

Grafik fungsi $T\left(x\right)=2x^3+3a{x}^2-4bx+5$ akan selalu turun dalam interval $-4<x<1$. Nilai $\frac{b}{a}$ adalah $\cdots \cdot$
A. $1$                    C. $3$                    E. $9$
B. $2$                    D. $6$

Pembahasan

Diketahui $T\left(x\right)=2x^3+3a{x}^2-4bx+5$

dan $T\left(x\right)$ selalu turun di $-4<x<1$, mengimplikasikan bahwa
$\begin{array}{cccc}(x+4)(x-1)& <0& & \\ x^2-x+4x-4& <0& & \\ x^2+3x-4& <0& & (\cdots 1)\end{array}$
Turunan pertama $T\left(x\right)$ adalah $T^{\prime }\left(x\right)=6x^2+6ax-4b$.
Grafik fungsi $T\left(x\right)$ selalu turun jika diberi syarat $T^{\prime }\left(x\right)<0$.
$\begin{array}{cccc}6x^2+6ax-4b& <0& & \\ \text{Kedua ruas dibagi}& \text{dengan}6& & \\ x^2+ax-\frac{2}{3}b& <0& & (\cdots 2)\end{array}$
Kaitkan pertidaksamaan $\left(1\right)$ dan $\left(2\right)$.
$\{\begin{array}{cc}{x}^2+3x-4& <0\\ x^2+ax-\frac{2}{3}b& <0\end{array}$
Diperoleh:
$\begin{array}{cc}a& =3\left(✓\right)\\ \bullet -\frac{2}{3}b& =-4\Rightarrow b=6\left(✓\right)\end{array}$
Jadi, nilai $\frac{b}{a}=\frac{6}{3}=2$

(Jawaban B)

Contoh Soal 8

Grafik fungsi $L\left(x\right)=a{x}^3+9b{x}^2-24x+5$ akan selalu naik dalam interval $x<-4$ atau $x>1$. Nilai $a+b$ adalah $\cdots \cdot$
A. $1$                    C. $3$                    E. $9$
B. $2$                    D. $6$

Pembahasan

Diketahui $L\left(x\right)=a{x}^3+9b{x}^2-24x+5$

dan $L\left(x\right)$ selalu naik di $x<-4$ atau $x>1$, mengimplikasikan bahwa
$\begin{array}{cccc}(x+4)(x-1)& >0& & \\ x^2-x+4x-4& >0& & \\ x^2+3x-4& >0& & (\cdots 1)\end{array}$
Turunan pertama $L\left(x\right)$ adalah $L^{\prime }\left(x\right)=3a{x}^2+18bx-24$.
Grafik fungsi $L\left(x\right)$ selalu naik jika diberi syarat $L^{\prime }\left(x\right)>0$.
$\begin{array}{cccc}3a{x}^2+18bx-24& >0& & \\ \text{Kedua ruas dibagi}& \text{dengan}6& & \\ \frac{a}{2}{x}^2+3bx-4& >0& & (\cdots 2)\end{array}$
Catatan: Mengapa harus dibagi 6? Karena kita harus membuat konstantanya menjadi $-4$ sesuai dengan pertidaksamaan $\left(1\right)$.
Berikutnya, kaitkan pertidaksamaan $\left(1\right)$ dan $\left(2\right)$.
$\{\begin{array}{cc}{x}^2+3x-4& >0\\ \frac{a}{2}{x}^2+3bx-4& >0\end{array}$
Diperoleh:
$\begin{array}{cc}\bullet \frac{a}{2}& =1\Rightarrow a=2\\ \bullet 3b& =3\Rightarrow b=1\end{array}$
Jadi, nilai $a+b=2+1=3$

(Jawaban C)

Contoh Soal 9

Fungsi $f\left(x\right)={\sin }^{2}x$

dengan $0<x<2\pi$ naik pada interval $\cdots \cdot$
A. $\frac{\pi }{2}<x<\pi$ atau $\frac{3\pi }{2}<x<2\pi$
B. $\frac{2\pi }{3}<x<\pi$
C. $0<x<\frac{\pi }{2}$ atau $\pi <x<\frac{3\pi }{2}$
D. $0<x<\pi$ atau $\pi <x<2\pi$
E. $0<x<2\pi$

Pembahasan

Diketahui $f\left(x\right)={\sin }^{2}x$

.
Turunan pertamanya adalah $f^{\prime }\left(x\right)=2\sin x\cos x=\sin 2x$. Grafik fungsi $f$ akan naik ketika diberi syarat $f^{\prime }\left(x\right)>0$, yaitu $\sin 2x>0$.
Pembuat nol adalah $\{0,\frac{\pi }{2},\pi ,\frac{3\pi }{2},2\pi \}$.
Buat garis bilangan dan tentukan tanda kepositivan dengan uji titik.

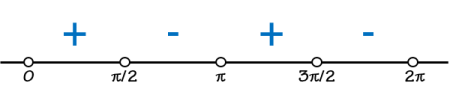
Ini berarti, $\sin 2x>0$ terpenuhi ketika $0<x<\frac{\pi }{2}$ atau $\pi <x<\frac{3\pi }{2}$. Jadi, $f\left(x\right)={\sin }^{2}x$ akan naik pada interval $0<x<\frac{\pi }{2}$ atau $\pi <x<\frac{3\pi }{2}$

, seperti yang dipertegas pada sketsa grafik berikut.
(Jawaban C)

Contoh Soal 10

Grafik fungsi $f\left(x\right)=x^3+a{x}^2+bx+c$ hanya turun pada interval $-1<x<5$. Nilai $a+b=\cdots \cdot$
A. $-21$                  C. $-9$                   E. $21$
B. $-15$                  D. $9$

Pembahasan

Diketahui $f\left(x\right)=x^3+a{x}^2+bx+c$

dan $f\left(x\right)$ selalu turun di $-1<x<5$, mengimplikasikan bahwa
$\begin{array}{cccc}(x+1)(x-5)& <0& & \\ x^2-5x+x-5& <0& & \\ x^2-4x-5& <0& & (\cdots 1)\end{array}$
Turunan pertama $f\left(x\right)$ adalah $f^{\prime }\left(x\right)=3x^2+2ax+b$.
Grafik fungsi $f\left(x\right)$ selalu turun jika diberi syarat $f^{\prime }\left(x\right)<0$.
$\begin{array}{cccc}3x^2+2ax+b& <0& & \\ \text{Kedua ruas dibagi}& \text{dengan}3& & \\ x^2+\frac{2}{3}ax+\frac{1}{3}b& <0& & (\cdots 2)\end{array}$
Kaitkan pertidaksamaan $\left(1\right)$ dan $\left(2\right)$.
$\{\begin{array}{cc}{x}^2-4x-5& <0\\ x^2+\frac{2}{3}ax+\frac{1}{3}b& <0\end{array}$
Diperoleh:
$\begin{array}{cc}\bullet \frac{2}{3}a& =-4\Rightarrow a=-6\\ \bullet \frac{1}{3}b& =-5\Rightarrow b=-15\end{array}$
Jadi, nilai $a+b=-6+(-15)=-21$
(Jawaban A)

Terima kasih kepada Ibu DR Lizza Novrida, semoga apa yang pelajari hari memberikan manfaat dikemudian hari dan diberkati tuhan yang maha esa.
Wassalamualaikum Warahmatullahi Wabarakatuh
Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam

 

SOURCE :

https://mathcyber1997.com/materi-soal-dan-pembahasan-fungsi-naik-dan-fungsi-turun/