Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam
Sebelum saya membahas, pembahasan kita hari ini. Yakni mengenai materi matematika wajib kelas 10, yaitu "Perbandingan Trigonometri". Saya akan memperkenalkan diri. Saya Paisal Vieri Eka Tama Simbolon murid kelas 10 di Sekolah Menengah Atas 63 Jakarta. Saya bukan siapa siapa, saya hanya menyukai hal yang pemerintahan atau mungkin juga dikatakan politik dengan seni dan manuver yang berlika-liku. Dan saya suka perubahan. Cukup tentang saya bisa follow instagram saya jika anda mau tentunya @paisalts_.
Kita bahas tentang "Perbandingan Trigonometri" kita harus tahu apa pengertian dari Trigonometri.
Trigonometri adalah ilmu matematika yang mempelajari tentang sudut, sisi, dan perbandingan antara sudut terhadap sisi. Dasarnya menggunakan bangun datar segitiga. Hal ini karena arti dari kata trigonometri sendiri yang dalam bahasa Yunani yang berarti ukuran-ukuran dalam sudut tiga atau segitiga.

Sisi AB merupakan sisi miring segitiga
Sisi BC merupakan sisi depan sudut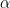
Sisi AC merupakan sisi samping sudut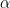
Di sini kita akan mengenal istilah matematika baru, yaitu sinus (sin), cosinus (cos), tangent (tan), cosecan (csc), secan (sec) dan cotangent (cot), yang mana sinus merupakan kebalikan dari cosecan, cosinus kebalikan dari secan dan tangent kebalikan dari cotangent.
 , sehingga bisa dihapal dengan sebutan sin-de-mi.
, sehingga bisa dihapal dengan sebutan sin-de-mi.
 , sehingga bisa dihapal dengan sebutan cos-sa-mi.
, sehingga bisa dihapal dengan sebutan cos-sa-mi.
 , sehingga bisa dihapal dengan sebutan tan-de-sa.
, sehingga bisa dihapal dengan sebutan tan-de-sa.
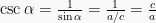 .
.
 .
.
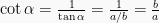
Sudut Istimewa
Trigonometri adalah ilmu matematika yang mempelajari tentang sudut, sisi, dan perbandingan antara sudut terhadap sisi. Dasarnya menggunakan bangun datar segitiga. Hal ini karena arti dari kata trigonometri sendiri yang dalam bahasa Yunani yang berarti ukuran-ukuran dalam sudut tiga atau segitiga.
Setelah mengetahui apa pengertian dari Trigonometri, barulah kita bahas tema kita hari ini, yakni "Perbandingan Trigonometri".
Perbandingan Trigonometri Pada Segitiga
Sebuah segitiga dengan salah satu sudutnya berupa : alfa
Sisi AB merupakan sisi miring segitiga
Sisi BC merupakan sisi depan sudut
Sisi AC merupakan sisi samping sudut
Di sini kita akan mengenal istilah matematika baru, yaitu sinus (sin), cosinus (cos), tangent (tan), cosecan (csc), secan (sec) dan cotangent (cot), yang mana sinus merupakan kebalikan dari cosecan, cosinus kebalikan dari secan dan tangent kebalikan dari cotangent.
Sinus, Cosinus dan Tangent digunakan untuk menghitung sudut dengan perbandingan trigonometri sisi di segitiga. Dengan gambar segitiga diatas, nilai Sinus, Cosinus dan Tangent diperoleh dengan cara sebagai berikut:
Sudut Istimewa
Berikut ini nilai sin, cos, dan tan untuk sudut istimewa:

Dalam Kuadran
Sudut dalam suatu lingkaran, memiliki rentang 0° – 360°, sudut tersebut dibagi menjadi 4 kuadran, dengan masing-masing kuadran memiliki rentang sebesar 90°.



Dalam suatu segitiga siku-siku, selalu berlaku prinsip phytagoras, yaitu . Pada materi ini, prinsip phytagoras ini menjadi asal pembuktian identitas trigonometri sendiri.
. Pada materi ini, prinsip phytagoras ini menjadi asal pembuktian identitas trigonometri sendiri.
 bagi kedua ruas dengan
bagi kedua ruas dengan 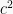 , diperoleh persamaan baru
, diperoleh persamaan baru  . Sederhanakan dengan sifat eksponensial menjadi
. Sederhanakan dengan sifat eksponensial menjadi  . Dari persamaan terakhir, subtitusi bagian yang sesuai dengan perbandingan trigonometri pada segitiga, yaitu
. Dari persamaan terakhir, subtitusi bagian yang sesuai dengan perbandingan trigonometri pada segitiga, yaitu  dan
dan  , sehingga diperoleh
, sehingga diperoleh  atau bisa ditulis menjadi
atau bisa ditulis menjadi  .
.
Dari identitas yang pertama, dapat diperoleh bentuk lainnya, yaitu:
 bagi kedua ruas dengan
bagi kedua ruas dengan  , diperoleh
, diperoleh  dimana
dimana  dan
dan 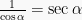 , sehingga diperoleh:
, sehingga diperoleh: 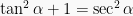
Bentuk ketiga yaitu dibagi dengan
dibagi dengan 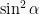 menjadi
menjadi 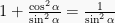 , dimana
, dimana  dan
dan  , sehingga diperoleh persamaan:
, sehingga diperoleh persamaan: 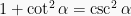 .
.
Jadi kita sudah mengetahui definisi umum dari "Perbandingan Trigonometri" sekarang mari kita lihat soal berikut ini.
Contoh Soal Trigonometri
1. Soal Nomor 4
Perhatikan gambar di bawah.

Segitiga ABC siku-siku di C. Pernyataan berikut ini benar, kecuali ⋯⋅
A. sin α = BC/AB
B. cos β = BC/AC
C. sin β = AC/AB
D. tan α = BC/AC
E. cos α = AC/AB
B. 2/5
C. 2/3
D. 2/5
E. 3/4

Dalam Kuadran
Sudut dalam suatu lingkaran, memiliki rentang 0° – 360°, sudut tersebut dibagi menjadi 4 kuadran, dengan masing-masing kuadran memiliki rentang sebesar 90°.

- Kuadran 1 memiliki rentang sudut dari 0° – 90° dengan nilai sinus, cosinus dan tangent positif.
- Kuadran 2 memiliki rentang sudut dari 90° – 180° dengan nilai cosinus dan tangen negatif, sinus positif.
- Kuadran 3 memiliki rentang sudut dari 180° – 270° dengan nilai sinus dan cosinus negatif, tangen positif.
- Kuadran 4 memiliki rentang sudut dari 270° – 360° dengan nilai sinus dan tangent negatif, cosinus positif.

Identitas Trigonometri

Dalam suatu segitiga siku-siku, selalu berlaku prinsip phytagoras, yaitu
Dari identitas yang pertama, dapat diperoleh bentuk lainnya, yaitu:
Bentuk ketiga yaitu
Jadi kita sudah mengetahui definisi umum dari "Perbandingan Trigonometri" sekarang mari kita lihat soal berikut ini.
Contoh Soal Trigonometri
1. Soal Nomor 4
Perhatikan gambar di bawah.

Segitiga ABC siku-siku di C. Pernyataan berikut ini benar, kecuali ⋯⋅
A. sin α = BC/AB
B. cos β = BC/AC
C. sin β = AC/AB
D. tan α = BC/AC
E. cos α = AC/AB
Pembahasan
Berdasarkan gambar di atas, perbandingan trigonometri untuk sinus, cosinus, dan tangen dari sudut α dan β adalah sebagai berikut.
=)sin α = de/mi = BC/AB
=)cos α = sa/mi = AC/AB
=)tan α = de/sa = BC/AC
=)sin β = de/mi = AC/AB
=)cos β = sa/mi = BC/AB
=)tan β = de/sa = AC/BC
Jadi, dari kelima pernyataan (pilihan) yang diberikan, pernyataan yang salah ada pada pilihan jawaban B.
=)sin α = de/mi = BC/AB
=)cos α = sa/mi = AC/AB
=)tan α = de/sa = BC/AC
=)sin β = de/mi = AC/AB
=)cos β = sa/mi = BC/AB
=)tan β = de/sa = AC/BC
Jadi, dari kelima pernyataan (pilihan) yang diberikan, pernyataan yang salah ada pada pilihan jawaban B.
2. Besar sudut 72° sama dengan ... rad
A. 1/5 B. 2/5
C. 2/3
D. 2/5
E. 3/4
Pembahasan
Ingat bahwa 1° = π/180 rad
Dengan demikian,
Dengan demikian,
72° =72^2 × π/180^5 rad
= 2/5 π rad
Jadi, besar sudut 72° sama dengan 2/5 π rad
(Jawaban C)
Oke, jadi sekarang kita sudah menguasai mengenai "Perbandingan Trigonometri. Semoga apa yang pelajari hari memberikan manfaat dikemudian hari dan diberkati tuhan yang maha esa.
Wassalamualaikum Warahmatullahi Wabarakatuh
Dengan demikian,
Dengan demikian,
72° =72^2 × π/180^5 rad
= 2/5 π rad
Jadi, besar sudut 72° sama dengan 2/5 π rad
(Jawaban C)
Oke, jadi sekarang kita sudah menguasai mengenai "Perbandingan Trigonometri. Semoga apa yang pelajari hari memberikan manfaat dikemudian hari dan diberkati tuhan yang maha esa.
Wassalamualaikum Warahmatullahi Wabarakatuh
Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan Salam Sejahtera Untuk Seluruh Alam



