Soal Kesamaan Matrik
Contoh Soal 1 :
Sebuah matriks P ordo 2 x 2 memenuhi persamaan menyerupai di bawah ini, tentukanlah matriks P.
Misalkan elemen-elemen matriks P ialah a, b, c, dan d
7 - 3a = -5 ---> -3a = -12 ---> a = 4
1 - 3b = 10 ---> -3b = 9 ---> b = -3
-4 - 3c = 8 ---> -3c = 12 ---> c = -4
3 - 3d = 9 ---> -3d = 6 ---> d = -2
Contoh Soal 2 :
Tentukan besar sudut a dan sudut b.
cos a = 2 + (-2) = 0 ---> a = 90
sin b = 3 + (2,5) = 0,5 = 1/2 ---> b = 30
Contoh Soal 3 :
Berdasarkan persamaan matriks di bawah ini, tentukanlah nilai a, b, c, dan d.
2d + d = -2 + (-4)
3d = -6
d = -2
a + 2d + 3 = 10 + 2
a + 2(-2) = 12 - 3
a - 4 = 9
a = 9 + 4
a = 13
b + b + 3c = 16 + 8
2b + 3c = 24
c - 2 + 2 + b = -6 + 6
c + b = 0 ---> c = -b ---> substitusi ke persamaan 2b + 3c = 24
2b + 3(-b) = 24
2b - 3b = 24
-b = 24
b = -24 maka c = 24
Makara a = 13. b = -24, c = 24, dan d = -2
Contoh Soal 4 :
Jika p, q, r, dan s memenuhi persamaan matriks
1. p - 2s = 1
2. 2q - r = 1
3. 2r - q = -1
4. s - 2p = -1
Dari persamaan no 1 dan 4 diperoleh :
p - 2s = 1 ---> p = 1 + 2s ---> substitusikan ke persamaan 4
s - 2p = -1
s - 2(1 + 2s) = -1
s - 2 - 4s = -1
-3s = 1
s = -1/3
selanjutnya,
p - 2(-1/3) = 1
p + 2/3 = 1
p = 1 - 2/3 = 1/3
Dari persamaan no 2 dan 3 diperoleh :
2q - r = 1 ---> -r = 1 - 2q ---> r = 2q + 1 ---> substitusi ke persamaan 3
2r - q = -1
2(2q + 1) - q = -1
4q + 2 - q = -1
3q = -3
q = -1
selanjutnya,
2(-1) - r = 1
-r = 1 + 2 = 3
r = -3
Makara p = 1/3, q = -1, r = -3 , dan s = -1/3
Contoh Soal 5 :
Diketahui persamaan matriks sebagai diberikut :
Pembahasan :
-a + 3 = 10 ---> a = -7
c - 2 + 10 = -6
c = - 6 - 8
c = -14
b + 4 + b + c = -6
2b + c = -10
2b - 14 = -10
2b = 4
b = 2
2d + d = b - 2
3d = 2 - 2
d = 0
Contoh Soal 6 :
Tentukan nilai x yang memenuhi persamaan matriks di bawah ini.
Dari relasi di atas, diperoleh
log (2a - 2) = 1
log (2a - 2) = log 10
2a - 2 = 10
a = 12/2 = 6
log (b-4) = log a
log (b-4) = log 6
b-4 = 6
b = 10
xlog a = log b
xlog 6 = log 10
xlog 6 = 1
x = 6
Makara nilai x yang memenuhi persamaan di atas ialah 6
Contoh Soal 7 :
-1 + 6 = 2 + 2x
5 = 2 + 2x
3 = 2x
x = 3/2
3 + 2 = 3 + z + 1
5 = 4 + z
z = 1
Soal Determinan Matriks Berordo 3 x 3 dan 2 x 2
Contoh Soal 1 :
Hitunglah berapa nilai determinan dari matriks ordo 2 x 2 berikut ini :
Jawaban untuk matriks ordo 2 x 2 di atas ialah seperti berikut ini :
Contoh Soal 2 :
Hitunglah berapa nilai determinan dari matriks ordo 3 x 3 berikut ini :
Jawaban untuk matriks ordo 3 x 3 di atas ialah seperti berikut ini :
det( A ) = ( 2 . 4 . 1 ) + ( 3 . 3 . 7 ) + ( 4 . 5 . 0 ) – ( 4 . 4 . 7 ) – ( 2 . 3 . 0 ) – ( 3 . 5 . 1 )
= ( 8 ) + ( 63 ) + ( 0 ) – ( 112 ) – ( 0 ) – 15
= – 56
Contoh Soal 3 :
Misalkan diketahui matriks A, yang merupakan matriks persegi dengan ordo dua.
Determinan matriks A dapat ditentukan dengan,
Untuk lebih memahami cara menentukkan determinan matriks ordo 2x2 perhatikan contoh berikut.
Penyelesaian:
Jadi determinan dari matriks B adalah 2
Contoh Soal 4 :
Misalkan diketahui matriks A, yang merupakan matriks persegi berordo tiga.
Determinan matriks A dapat ditentukan dengan langkah-langkah berikut.
Untuk lebih jelasnya perhatikan gambar berikut.
Jadi determinan dari matriks C adalah -32
Contoh Soal 5 :
Berapakah determinan dari matriks di bawah ini?
Solusi:
Sama dengan soal yang pertama, kita bisa menggunakan rumus untuk bisa menyelesaikannya.
Det (A) = |A| = ad – bc
|A| = (7 x 3) – (2 x 8)
|A| = 21 – 16
|A| = 5
Contoh Soal 6 :
Hitunglah berapa nilai determinan dari matriks ordo 2 x 2 berikut ini :
Jawaban untuk matriks ordo 2 x 2 di atas ialah seperti berikut ini :
Contoh Soal 7 :
Berapakah determinan dari matriks di bawah ini?
Solusi:
Untuk menyelesaikan soal di atas, maka kita akan menggunakan aturan Sarrus.
|A| = aei + bfg + cdh – ceg – afh – bdi
|A| = (2x5x1) + (4x2x2) + (1x3x3) – (1x5x2) – (2x2x3) – (4x3x1)
|A| = 10 + 16 + 9 – 10 – 12 – 12
|A| = 1
Soal Kofaktor Matriks Berordo 3 x 3 dan 2 x 2
Contoh Soal 1 :
Rumus:
Penyelesaian:
Contoh Soal 2 :
Tentukan determinan matriks berikut!
Pembahasan
- A11 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-1.
- A12 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-2.
- A13 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-3.
Sehingga,
Contoh Soal 3 :
Invers Matriks Berordo 3 x 3 dan 2 x 2
Contoh Soal 1 :
Tentukanlah invers dari matriks berikut.
Pembahasan:
Catatan: elemen-elemen
yang berada di lingkar biru merupakan diagonal utama matriks A yang
ditukar posisinya, sedangkan elemen-elemen yang berada di lingkar oranye
merupakan diagonal kedua matriks A yang dikalikan dengan minus satu
(-1).
Contoh Soal 2 :
Tentukan invers matriks berikut dengan menggunakan adjoin!
Penyelesaian:
Oke, berdasarkan rumus di atas, kita membutuhkan determinan dan adjoin matriks A. Pertama, kita cari terlebih dahulu determinan matriks A menggunakan metode yang sudah dijelaskan sebelumnya. Bisa dengan cara aturan Sarrus ataupun metode minor-kofaktor. Misalnya, kita akan menggunakan metode Sarrus, sehingga:
Kemudian, kita tentukan adjoin matriks dengan mencari kofaktor matriks A tersebut.
Oleh karena itu,
Jadi,
Contoh Soal 3 :
Menentukan matriks invers dari!
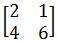
Jawaban :
Untuk menghitung kebalikan dari matriks, metode cepat digunakan. Sebelum menggunakan rumus matriks terbalik di atas. Pertama-tama kita harus menemukan nilai adjoin dahulu.
Untuk menemukan matriks invers 2×2 yang berdekatan, kita hanya perlu menukar atau memindahkan elemen yang posisinya ada di baris pertama kolom pertama dengan elemen-elemen di baris kedua kolom kedua.
Berikutnya, baris kedua dari kolom pertama dan baris pertama dari kolom kedua dikalikan dengan -1. Hasilnya adalah sebagai berikut.
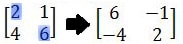
Selanjutnya, cari determinan matriks
det = (2 × 6) – (4 × 1)
= 12 – 4
= 8
Setelah nilai adjoin dan determinan matriks diketahui. Kemudian masukkan rumus matriks di atas. Hasilnya adalah :
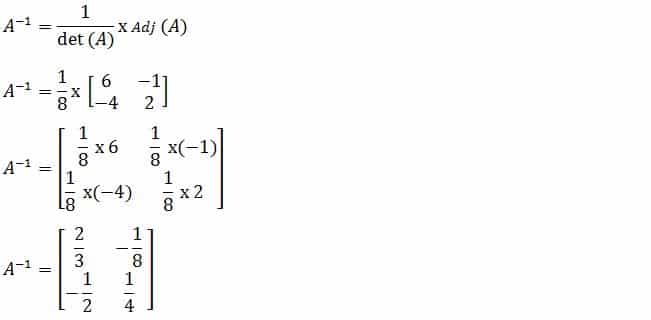
Contoh Soal 4 :
Matriks A dikenal sebagai berikut :
Jawaban :
Wassalamualaikum Warahmatullahi Wabarakatuh
Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam
Admin. (n.d.). Menentukan Determinan Matriks Berordo 2x2 dan 3x3 . Retrieved September 7, 2020, from www.madematika.net: https://www.madematika.net/2015/08/menentukan-determinan-matriks-berordo.html
Admin. (n.d.). Soal Dan Pembahasan Kesamaan Matriks. Retrieved September 7, 2020, from mataseluruhdunia208.blogspot.com: https://mataseluruhdunia208.blogspot.com/2018/06/soal-dan-pembahasan-kesamaan-matriks.html
Ammariah, H. (2019, 7 Desember). Matematika Kelas 11 | Cara Mencari Determinan dan Invers Matriks. Retrieved September 7, 2020, from blog.ruangguru.com: https://blog.ruangguru.com/cara-mencari-determinan-dan-invers-matriks
Baru, G. (2020, Mei 5). Invers Matriks. Retrieved September 7, 2020, from rumusrumus.com: https://rumusrumus.com/invers-matriks/
Isetiabhakti. (2019, Oktober 10). Mencari Determinan Matriks (3×3) Dengan Metode Ekspansi Kofaktor. Retrieved Sepember 7, 2020, from medium.com: https://medium.com/@isetiabhakti/mencari-determinan-matriks-3-3-dengan-metode-ekspansi-kofaktor-cad6afd0f57d
Pintar, K. (2020, Juni 20). Cara Mencari Determinan Matriks yang Mudah. Retrieved September 7, 2020, from www.kelaspintar.id: https://www.kelaspintar.id/blog/tips-pintar/cara-mencari-determinan-matriks-yang-mudah-5484/
Rahmah, A. (2020, Januari 18). Determinan Matriks Ordo 2×2 3×3 nxn dan Contoh Soalnya. Retrieved September 7, 2020, from rumus.co.id: https://rumus.co.id/determinan-matriks/
Tidak ada komentar:
Posting Komentar