INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA

Paisal Vieri Eka Tama Simbolon (28) XI IPS 2

Shalom

Om Swastiastu 

Namo Buddhaya 

Rahayu 

Salam Kebajikan 

Salam Sejahtera Untuk Seluruh Alam

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

ﺇِﻥَّ ﺍﻟْﺤَﻤْﺪَ ﻟِﻠَّﻪِ ﻧَﺤْﻤَﺪُﻩُ ﻭَﻧَﺴْﺘَﻌِﻴْﻨُﻪُ ﻭَﻧَﺴْﺘَﻐْﻔِﺮُﻩْ ﻭَﻧَﻌُﻮﺫُ ﺑِﺎﻟﻠﻪِ ﻣِﻦْ ﺷُﺮُﻭْﺭِ ﺃَﻧْﻔُﺴِﻨَﺎ ﻭَﻣِﻦْ ﺳَﻴِّﺌَﺎﺕِ ﺃَﻋْﻤَﺎﻟِﻨَﺎ، ﻣَﻦْ ﻳَﻬْﺪِﻩِ ﺍﻟﻠﻪُ ﻓَﻼَ ﻣُﻀِﻞَّ ﻟَﻪُ ﻭَﻣَﻦْ ﻳُﻀْﻠِﻞْ ﻓَﻼَ ﻫَﺎﺩِﻱَ ﻟَﻪُ. ﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻻَ ﺇِﻟَﻪَ ﺇِﻻَّ ﺍﻟﻠﻪ ﻭَﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻣُﺤَﻤَّﺪًﺍ ﻋَﺒْﺪُﻩُ ﻭَﺭَﺳُﻮْﻟُﻪُ.

Saya akan memperkenalkan diri. Saya Paisal Vieri Eka Tama Simbolon (28) murid kelas XI IPS 2 di Sekolah Menengah Atas Negeri 63 Jakarta. 

 

 

Tegalwangi

Source : GNFI

Integral Tak Tentu

 

Uraian

 

Bagaimana kita menyatakan suatu bentuk integral suatu fungsi? Notasi matematika yang digunakan untuk menyatakan integral adalah , seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan) dan dibaca �integral�.

Pengintegralan fungsi f(x) yang ditulis sebagai f(x) dx disebut integral tak tentu dari f(x). Jika F(x) anti turunan dari f(x), maka

 

 

Keterangan:

: notasi integral (yang diperkenalkan oleh Leibniz, seorang matematikawan Jerman)

f(x): fungsi integran

f(x): fungsi integral umum yang bersifat f"(x) = F(x)

c : konstanta pengintegralan

 

Sekarang, perhatikan turunan fungsi-fungsi berikut.

 

Dari uraian ini, tampak bahwa jika maka atau dapat dituliskan

 

Sebagai contoh, turunan fungsi f(x) = 2x² + c adalah f'(x) = 4x. Ini berarti, antiturunan dari f'(x) = 4x adalah f(x) = 2x² + c atau dituliskan f(xdx) = 2x² + c.

 

Uraian ini menggambarkan hubungan berikut.

Jika f'(x) = xⁿ , maka dengan c suatu konstanta.

Sehingga sifat-sifat integral yang berlaku memenuhi aturan sebagai berikut:

 

 

 

Perhatikan pangkat dan koefisien dari masing-masing soal berikut.

Contoh

 

Jawab:

Koefisien dapat kita keluarkan dari tanda integral.

 

 

Jawab:

Lakukan perkalian suku-suku persoalan terlebih dahulu pada soal:

 

 

Jawab:

 

 

Jawab:

 

Ada fungsi yang tidak dapat kita integralkan dengan konsep integral yang kita peroleh yaitu pada eksponen dengan pangkat n = �1.

Untuk itu, perhatikan bentuk soal berikut:

 

 

Karena bentuk penyebut sama dengan nol (0) menyebabkan hasil tak berhingga. Sehingga bentuk integral tersebut digolongkan bentuk integral khusus.

 

 

Oleh karena itu, untuk Integral khusus tersebut berlaku aturan:

 

 

Agar lebih menguasai materi tersebut, Anda diberikan beberapa contoh soal tentang integral khusus.

 

Contoh Soal :

Contoh Soal 1

Contoh Soal 2

Tentukan hasil dari ʃ 3x² dx !

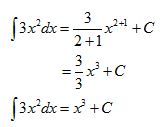
Jadi, hasil dari ʃ 3x² dx adalah x³ + C.

Contoh Soal 3

Carilah hasil integral tak tentu dari ʃ 8x³ – 6x² + 4x – 2 dx.

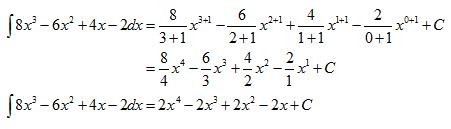
Jadi hasil dari ʃ 8x³ – 6x² + 4x – 2 dx adalah 2x⁴ – 2x³ + 2x² – 2x + C.

Contoh Soal 4

Tentukan nilai dari ʃ 4 sin x + 7 cos x dx !

ʃ sin x dx = – cos x + C

ʃ cos x dx = sin x + C

Maka:

ʃ 4 sin x + 7 cos x dx = – 4cos x + 7sin x + C

Jadi, nilai dari nilai dari ʃ 4 sin x + 7 cos x dx adalah – 4cos x + 7sin x + C.

Contoh Soal 5

Carilah nilai dari ʃ (3x-2)(x+6) dx

(3x-2)(x+6) = 3x² + 18x – 2x -12 = 3x² + 16x -12

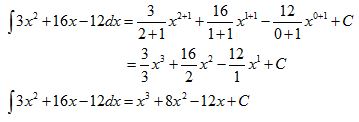
Jadi, hasil dari ʃ (3x-2)(x+6) dx adalah x³ + 8x² – 12x + C.

Terima kasih kepada Ibu DR Lizza Novrida, semoga apa yang pelajari hari memberikan manfaat dikemudian hari dan diberkati tuhan yang maha esa.
Wassalamualaikum Warahmatullahi Wabarakatuh
Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam

DAFTAR PUSTAKA

Admin. (n.d.). Integral Tak Tentu. Retrieved from sumberbelajar.belajar.kemdikbud.go.id: https://sumberbelajar.belajar.kemdikbud.go.id/sumberbelajar/tampil/Integral-Tak-Tentu-/konten10.html

Kevin. (2021, Maret 8). Contoh Soal Integral Tentu, Tak tentu, Parsial & Pembahasannya. Retrieved from rumuspintar.com: https://rumuspintar.com/integral/contoh-soal/#Contoh_Soal_Integral_Tak_Tentu