TRANSFORMASI : TRANSLASI, REFLEKSI, ROTASI DAN DILATASI

 Salam Sejahtera Untuk Seluruh Alam

Shalom

Om Swastiastu 

Namo Buddhaya 

Rahayu 

Salam Kebajikan 

Salam Sejahtera Untuk Seluruh Alam

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

ﺇِﻥَّ ﺍﻟْﺤَﻤْﺪَ ﻟِﻠَّﻪِ ﻧَﺤْﻤَﺪُﻩُ ﻭَﻧَﺴْﺘَﻌِﻴْﻨُﻪُ ﻭَﻧَﺴْﺘَﻐْﻔِﺮُﻩْ ﻭَﻧَﻌُﻮﺫُ ﺑِﺎﻟﻠﻪِ ﻣِﻦْ ﺷُﺮُﻭْﺭِ ﺃَﻧْﻔُﺴِﻨَﺎ ﻭَﻣِﻦْ ﺳَﻴِّﺌَﺎﺕِ ﺃَﻋْﻤَﺎﻟِﻨَﺎ، ﻣَﻦْ ﻳَﻬْﺪِﻩِ ﺍﻟﻠﻪُ ﻓَﻼَ ﻣُﻀِﻞَّ ﻟَﻪُ ﻭَﻣَﻦْ ﻳُﻀْﻠِﻞْ ﻓَﻼَ ﻫَﺎﺩِﻱَ ﻟَﻪُ. ﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻻَ ﺇِﻟَﻪَ ﺇِﻻَّ ﺍﻟﻠﻪ ﻭَﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻣُﺤَﻤَّﺪًﺍ ﻋَﺒْﺪُﻩُ ﻭَﺭَﺳُﻮْﻟُﻪُ.

Saya akan memperkenalkan diri. Saya Paisal Vieri Eka Tama Simbolon (27) murid kelas XI IPS 2 di Sekolah Menengah Atas Negeri 63 Jakarta. Dan saya suka perubahan. Follow instagram @paisalts_.

 

LANGSUNG YAKK...................

Jadi sekarang kita sudah menguasai berbagai macam soal Semoga apa yang pelajari hari memberikan manfaat dikemudian hari dan diberkati tuhan yang maha esa.
Wassalamualaikum Warahmatullahi Wabarakatuh
Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam

Soal Cerita dan Penyelesaiannya dengan Bantuan Determinan dan Invers Matriks

 

 

Salam Sejahtera Untuk Seluruh Alam

Shalom

Om Swastiastu 

Namo Buddhaya 

Rahayu 

Salam Kebajikan 

Salam Sejahtera Untuk Seluruh Alam

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

ﺇِﻥَّ ﺍﻟْﺤَﻤْﺪَ ﻟِﻠَّﻪِ ﻧَﺤْﻤَﺪُﻩُ ﻭَﻧَﺴْﺘَﻌِﻴْﻨُﻪُ ﻭَﻧَﺴْﺘَﻐْﻔِﺮُﻩْ ﻭَﻧَﻌُﻮﺫُ ﺑِﺎﻟﻠﻪِ ﻣِﻦْ ﺷُﺮُﻭْﺭِ ﺃَﻧْﻔُﺴِﻨَﺎ ﻭَﻣِﻦْ ﺳَﻴِّﺌَﺎﺕِ ﺃَﻋْﻤَﺎﻟِﻨَﺎ، ﻣَﻦْ ﻳَﻬْﺪِﻩِ ﺍﻟﻠﻪُ ﻓَﻼَ ﻣُﻀِﻞَّ ﻟَﻪُ ﻭَﻣَﻦْ ﻳُﻀْﻠِﻞْ ﻓَﻼَ ﻫَﺎﺩِﻱَ ﻟَﻪُ. ﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻻَ ﺇِﻟَﻪَ ﺇِﻻَّ ﺍﻟﻠﻪ ﻭَﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻣُﺤَﻤَّﺪًﺍ ﻋَﺒْﺪُﻩُ ﻭَﺭَﺳُﻮْﻟُﻪُ.

Sebelum saya membahas "Soal Cerita dan Penyelesaiannya dengan Bantuan Determinan dan Invers Matriks", Saya akan memperkenalkan diri. Saya Paisal Vieri Eka Tama Simbolon (27) murid kelas XI IPS 2 di Sekolah Menengah Atas Negeri 63 Jakarta. Dan saya suka perubahan. Follow instagram @paisalts_.

 

SKUYYYYYYYYYYYYY.....................

 

Soal Cerita dan Penyelesaiannya dengan Bantuan Determinan dan Invers Matriks

 

Contoh Soal 1 :

Ani adalah seorang pengusaha makanan ringan yang menyetorkan dagangannya ke tiga kantin sekolah. Tabel berikut menyatakan jenis dan kuantitas makanan (dalam satuan bungkus) yang disetorkan setiap harinya di tiga kantin sekolah tersebut.

Harga Kacang, Keripik, Kuaci berturut-turut;

Kantin A : 10, 10, 5

Kantin B : 20, 15, 8

Kantn C : 15, 20, 10

 

Harga sebungkus kacang, sebungkus keripik, dan sebungkus permen masing-masing adalah Rp2.000,00, Rp3.000,00, dan Rp1.000,00. Hitunglah pemasukan harian yang diterima Bu Ani dari setiap kantin dalam bentuk matriks serta total pemasukan hariannya.

 

Misalkan $A$ adalah matriks yang entri-entrinya menyatakan kuantitas makanan yang disetorkan ke masing-masing kantin (baris pertama untuk kantin A, baris kedua untuk kantin B, dan baris ketiga untuk kantin C), sehingga
$A=\left(\begin{array}{ccc}10& 10& 5\\ 20& 15& 8\\ 15& 20& 10\end{array}\right)$
Misalkan juga $B$ adalah matriks yang menyatakan harga tiap makanan per bungkusnya, sehingga
$B=\left(\begin{array}{c}2.000\\ 3.000\\ 1.000\end{array}\right)$
Dengan demikian, hasil kali matriks $A$ dan $B$ menyatakan penghasilan Bu Ani untuk masing-masing kantin, yaitu
$$\begin{array}{cc}AB& =\left(\begin{array}{ccc}10& 10& 5\\ 20& 15& 8\\ 15& 20& 10\end{array}\right)\left(\begin{array}{c}2.000\\ 3.000\\ 1.000\end{array}\right)\\ & =\left(\begin{array}{c}(10\times 2.000)+(10\times 3.000)+(5\times 1.000)\\ (20\times 2.000)+(15\times 3.000)+(8\times 1.000)\\ (16\times 2.000)+(20\times 3.000)+(10\times 1.000)\end{array}\right)\\ & =\left(\begin{array}{c}20.000+30.000+5.000\\ 40.000+45.000+8.000\\ 30.000+60.000+10.000\end{array}\right)\\ & =\left(\begin{array}{c}55.000\\ 93.000\\ 100.000\end{array}\right)\end{array}$$Jadi, penghasilan Bu Ani yang diterima dari Kantin A, B, dan C berturut-turut adalah Rp55.000,00, Rp93.000,00, dan Rp100.000,00.
Total penghasilannya adalah
Rp55.000,00 + Rp93.000,00 + Rp100.000,00 = Rp248.000,00.

 

 

Contoh Soal 2 :

Arman membeli 5 pensil dan 3 penghapus, sedangkan Susi membeli 4 pensil dan 2 penghapus di toko yang sama. Di kasir, Arman membayar Rp 11.500,00 sedangkan Susi membayar Rp 9.000,00. Jika Dodi membeli 6 pensil dan 5 penghapus, berapa ia harus membayar?

Persoalan ini dapat diselesaikan menggunakan dua cara.

Jika maka dengan cara pertama, yakni cara invers, diperoleh .

Ingat, determinan dari adalah ad - bc.

Penyelesaian cara kedua adalah cara determinan, yaitu:

Penyelesaian

Dimisalkan harga satuan pensil = x dan harga satuan penghapus = y. Disusun ke dalam sistim persamaan linear dua variabel (SPLDV)

5x + 3y = 11.500

4x + 2y = 9.000

Sistim persamaan di atas dapat dinyatakan dalam bentuk matriks, yakni

Cara Pertama (Invers Matriks)

 

 

 

dan

Diperoleh harga satuan pensil Rp 2.000 dan harga satuan penghapus Rp 500.

Jadi, Dodi harus membayar [6 x Rp 2.000] + [5 x Rp 500] = Rp 14.500

-------------------------

Cara Kedua (Determinan Matriks)

Jadi, Dodi harus membayar [6 x Rp 2.000] + [5 x Rp 500] = Rp 14.500.

Contoh Soal 3 :

 

 

Ani membeli 3 kg jeruk, 1 kg apel dan 1 kg alpukat dengan harga Rp61.000,00. Ida membeli 2 kg jeruk, 2 kg apel dan 1 kg alpukat dengan harga Rp67.000,00. Wati membeli 1 kg jeruk, 3 kg apel dan 2 kg alpukat dengan harga Rp80.000,00. Jika mereka bertiga membeli buah di toko yang sama, berapakah harga 1 kg dari masing-masing dari buah tersebut?

.

Jawab

.

Misal  

x = harga 1 kg jeruk

y = harga 1 kg apel

z = harga 1 kg alpukat

.

Bentuk sistem persamaan linear tiga variabelnya

3x + y + z = 61.000

2x + 2y + z = 67.000

x + 3y + 2z = 80.000

.

Bentuk matriksnya

A =  

Kita tentukan matriks minornya

M =  

C =  

Adjoin A =  

Untuk menentukan determinan A, kita gunakan cara kofaktor dengan baris 1

det A = a₁₁.C₁₁ + a₁₂.C₁₂ + a₁₃.C₁₃

det A = 3(1) + 1(-3) + 1(4)

det A = 4

maka

X = A⁻¹ . B

Jadi  

harga 1 kg jeruk = Rp12.000,00

harga 1 kg apel = Rp18.000,00

harga 1 kg alpukat = Rp7.000,00

Oke, jadi sekarang kita sudah menguasai Soal Cerita dan Penyelesaiannya dengan Bantuan Determinan dan Invers Matriks. Semoga apa yang pelajari hari memberikan manfaat dikemudian hari dan diberkati tuhan yang maha esa.
Wassalamualaikum Warahmatullahi Wabarakatuh
Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam    

DAFTAR PUSTAKA

arsetpopeye. (2017, Desember 23). Retrieved September 14, 2020, from brainly.co.id: https://brainly.co.id/tugas/13775326

hakimium. (2014, November 17). Retrieved September 2020, 14, from brainly.co.id: https://brainly.co.id/tugas/1476814

Sukardi. (2019, Februari 10). Soal dan Pembahasan Super Lengkap – Matriks, Determinan, dan Invers Matriks. Retrieved September 14, 2020, from mathcyber1997.com: https://mathcyber1997.com/soal-dan-pembahasan-matriks-determinan-dan-invers-matriks/

 

SOAL PENYELESAIAN MATRIKS

 

Salam Sejahtera Untuk Seluruh Alam

Shalom

Om Swastiastu 

Namo Buddhaya 

Rahayu 

Salam Kebajikan 

Salam Sejahtera Untuk Seluruh Alam

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

ﺇِﻥَّ ﺍﻟْﺤَﻤْﺪَ ﻟِﻠَّﻪِ ﻧَﺤْﻤَﺪُﻩُ ﻭَﻧَﺴْﺘَﻌِﻴْﻨُﻪُ ﻭَﻧَﺴْﺘَﻐْﻔِﺮُﻩْ ﻭَﻧَﻌُﻮﺫُ ﺑِﺎﻟﻠﻪِ ﻣِﻦْ ﺷُﺮُﻭْﺭِ ﺃَﻧْﻔُﺴِﻨَﺎ ﻭَﻣِﻦْ ﺳَﻴِّﺌَﺎﺕِ ﺃَﻋْﻤَﺎﻟِﻨَﺎ، ﻣَﻦْ ﻳَﻬْﺪِﻩِ ﺍﻟﻠﻪُ ﻓَﻼَ ﻣُﻀِﻞَّ ﻟَﻪُ ﻭَﻣَﻦْ ﻳُﻀْﻠِﻞْ ﻓَﻼَ ﻫَﺎﺩِﻱَ ﻟَﻪُ. ﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻻَ ﺇِﻟَﻪَ ﺇِﻻَّ ﺍﻟﻠﻪ ﻭَﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻣُﺤَﻤَّﺪًﺍ ﻋَﺒْﺪُﻩُ ﻭَﺭَﺳُﻮْﻟُﻪُ.

Sebelum saya membahas "SOAL PENYELESAIAN MATRIKS", Saya akan memperkenalkan diri. Saya Paisal Vieri Eka Tama Simbolon (27) murid kelas XI IPS 2 di Sekolah Menengah Atas Negeri 63 Jakarta. Dan saya suka perubahan. Follow instagram @paisalts_.

 

LANGSUNG AJAA YOKKK.....................

 

Soal Kesamaan Matrik

Contoh Soal 1 : 

Sebuah matriks P ordo 2 x 2 memenuhi persamaan menyerupai di bawah ini, tentukanlah matriks P.

Pembahasan :
Misalkan elemen-elemen matriks P ialah a, b, c, dan d

7 - 3a = -5  ---> -3a = -12 ---> a = 4
1 - 3b = 10 ---> -3b = 9 ---> b = -3
-4 - 3c = 8 ---> -3c = 12 ---> c = -4
3 - 3d = 9 ---> -3d = 6 ---> d = -2

Contoh Soal 2 :

Tentukan besar sudut a dan sudut b.

Pembahasan :
cos a = 2 + (-2) = 0 ---> a = 90
sin b = 3 + (2,5) = 0,5 = 1/2 ---> b = 30

Contoh Soal 3 :

Berdasarkan persamaan matriks di bawah ini, tentukanlah nilai a, b, c, dan d.

Pembahasan :
2d + d = -2 + (-4)
3d = -6
d = -2

a + 2d + 3 = 10 + 2
a + 2(-2) = 12 - 3
a - 4  = 9
a = 9 + 4
a = 13

b + b + 3c = 16 + 8
2b + 3c = 24

c - 2 + 2 + b = -6 + 6
c + b = 0 ---> c = -b ---> substitusi ke persamaan 2b + 3c = 24
2b + 3(-b) = 24
2b - 3b = 24
-b = 24
b = -24 maka c = 24

Makara a = 13. b = -24, c = 24, dan d = -2

Contoh Soal 4 :

Jika p, q, r, dan s memenuhi persamaan matriks 

Pembahasan :

Dari soal, diperoleh 4 persamaan yaitu :
1. p - 2s = 1
2. 2q - r = 1
3. 2r - q = -1
4. s - 2p = -1

Dari persamaan no 1 dan 4 diperoleh :
p - 2s = 1 ---> p = 1 + 2s ---> substitusikan ke persamaan 4
s - 2p = -1
s - 2(1 + 2s) = -1
s - 2 - 4s = -1
-3s = 1
s = -1/3

selanjutnya,
p - 2(-1/3) = 1
p + 2/3 = 1
p = 1 - 2/3 = 1/3

Dari persamaan no 2 dan 3 diperoleh :
2q - r = 1 ---> -r = 1 - 2q ---> r = 2q + 1 ---> substitusi ke persamaan 3
2r - q = -1
2(2q + 1) - q = -1
4q + 2 - q = -1
3q = -3
q = -1

selanjutnya,
2(-1) - r = 1
-r = 1 + 2 = 3
r = -3

Makara p = 1/3, q = -1, r = -3 , dan s = -1/3

Contoh Soal 5 : 

Diketahui persamaan matriks sebagai diberikut :

Tentukanlah nilai a, b, c, dan d.

Pembahasan :
-a + 3 = 10 ---> a = -7

c - 2 + 10 = -6
c = - 6 - 8
c = -14

b + 4 + b + c = -6
2b + c = -10
2b - 14 = -10
2b = 4
b = 2

2d + d = b - 2
3d = 2 - 2
d = 0

Contoh Soal 6 :
Tentukan nilai x yang memenuhi persamaan matriks di bawah ini.

Pembahasan :
Dari relasi di atas, diperoleh
log (2a - 2) = 1
log (2a - 2) = log 10
2a - 2 = 10
a = 12/2 = 6

log (b-4) = log a
log (b-4) = log 6
b-4 = 6
b = 10

^xlog a = log b
^xlog 6 = log 10
^xlog 6 = 1
x = 6

Makara nilai x yang memenuhi persamaan di atas ialah 6

Contoh Soal 7 :

Tentukanlah nilai x dan z yang memenuhi persamaan matriks diberikut ini :

Pembahasan :
-1 + 6 = 2 + 2x
5 = 2 + 2x
3 = 2x
x = 3/2

3 + 2 = 3 + z + 1
5 = 4 + z
z = 1

Soal Determinan Matriks Berordo 3 x 3 dan 2 x 2

Contoh Soal 1 :

Hitunglah berapa nilai determinan dari matriks ordo 2 x 2 berikut ini :

Jawaban untuk matriks ordo 2 x 2 di atas ialah seperti berikut ini :

Contoh Soal 2 :

Hitunglah berapa nilai determinan dari matriks ordo 3 x 3 berikut ini :

Jawaban untuk matriks ordo 3 x 3 di atas ialah seperti berikut ini :

det( A ) = ( 2 . 4 . 1 ) + ( 3 . 3 . 7 ) + ( 4 . 5 . 0  ) – ( 4 . 4 . 7  ) – ( 2 . 3 . 0 ) – ( 3 . 5 . 1 ) 
               =      ( 8 )       +    ( 63 )     +       ( 0 )       –     ( 112 )     –      ( 0 )       –     15
               = – 56

Contoh Soal 3 :

Misalkan diketahui matriks A, yang merupakan matriks persegi dengan ordo dua.

Determinan matriks A dapat ditentukan dengan,

Untuk lebih memahami cara menentukkan determinan matriks ordo 2x2 perhatikan contoh berikut.

 

Tentukan determinan matriks 
Penyelesaian:

Jadi determinan dari matriks B adalah 2

Contoh Soal 4 :

Misalkan diketahui matriks A, yang merupakan matriks persegi berordo tiga.

Determinan matriks A dapat ditentukan dengan langkah-langkah berikut.
Untuk lebih jelasnya perhatikan gambar berikut.

Agar lebih memahaminya, perlajari contoh soal berikut.

Tentukan determinan matriks  

Penyelesaian:

Jadi determinan dari matriks C adalah -32

Contoh Soal 5 :

Berapakah determinan dari matriks di bawah ini?

Solusi:

Sama dengan soal yang pertama, kita bisa menggunakan rumus untuk bisa menyelesaikannya.

Det (A) = |A| = ad – bc

|A| = (7 x 3) – (2 x 8)

|A| = 21 – 16

|A| = 5

Contoh Soal 6 :

Hitunglah berapa nilai determinan dari matriks ordo 2 x 2 berikut ini :

Jawaban untuk matriks ordo 2 x 2 di atas ialah seperti berikut ini :

 

Contoh Soal 7 :

Berapakah determinan dari matriks di bawah ini?

Solusi:

Untuk menyelesaikan soal di atas, maka kita akan menggunakan aturan Sarrus.

|A| = aei + bfg + cdh – ceg – afh – bdi

|A| = (2x5x1) + (4x2x2) + (1x3x3) – (1x5x2) – (2x2x3) – (4x3x1)

|A| = 10 + 16 + 9 – 10 – 12 – 12

|A| = 1

Soal Kofaktor Matriks Berordo 3 x 3 dan 2 x 2

Contoh Soal 1 :

Rumus:

 

Penyelesaian:

Contoh Soal 2 :

Tentukan determinan matriks berikut!

Pembahasan

• A11 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-1.
• A12 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-2.
• A13 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-3.

Sehingga,

Contoh Soal 3 :

 

Invers Matriks Berordo 3 x 3 dan 2 x 2  

Contoh Soal 1 :

Tentukanlah invers dari matriks berikut.

Pembahasan:

 

Catatan: elemen-elemen yang berada di lingkar biru merupakan diagonal utama matriks A yang ditukar posisinya, sedangkan elemen-elemen yang berada di lingkar oranye merupakan diagonal kedua matriks A yang dikalikan dengan minus satu (-1).

Contoh Soal 2 :

Tentukan invers matriks berikut dengan menggunakan adjoin!

Penyelesaian:

 

Oke, berdasarkan rumus di atas, kita membutuhkan determinan dan adjoin matriks A. Pertama, kita cari terlebih dahulu determinan matriks A menggunakan metode yang sudah dijelaskan sebelumnya. Bisa dengan cara aturan Sarrus ataupun metode minor-kofaktor. Misalnya, kita akan menggunakan metode Sarrus, sehingga:

Kemudian, kita tentukan adjoin matriks dengan mencari kofaktor matriks A tersebut.

Oleh karena itu,

Jadi,

Contoh Soal 3 :

Menentukan matriks invers dari!

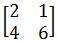
Jawaban :

Untuk menghitung kebalikan dari matriks, metode cepat digunakan. Sebelum menggunakan rumus matriks terbalik di atas. Pertama-tama kita harus menemukan nilai adjoin dahulu.

Untuk menemukan matriks invers 2×2 yang berdekatan, kita hanya perlu menukar atau memindahkan elemen yang posisinya ada di baris pertama kolom pertama dengan elemen-elemen di baris kedua kolom kedua.

Berikutnya, baris kedua dari kolom pertama dan baris pertama dari kolom kedua dikalikan dengan -1. Hasilnya adalah sebagai berikut.

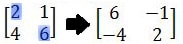
Selanjutnya, cari determinan matriks
det = (2 × 6) – (4 × 1)
= 12 – 4
= 8

Setelah nilai adjoin dan determinan matriks diketahui. Kemudian masukkan rumus matriks di atas. Hasilnya adalah :

Contoh Soal 4 :

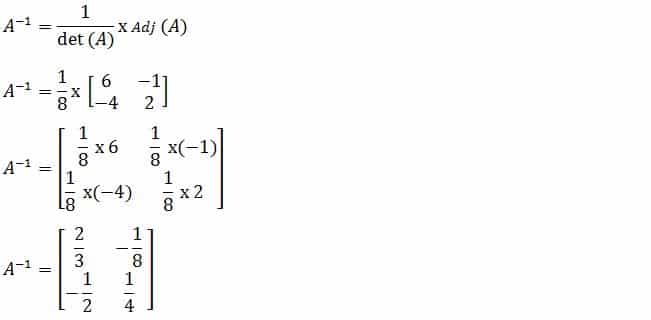
Matriks A dikenal sebagai berikut :

Jawaban :

Oke, jadi sekarang kita sudah menguasai berbagai macam soal Semoga apa yang pelajari hari memberikan manfaat dikemudian hari dan diberkati tuhan yang maha esa.
Wassalamualaikum Warahmatullahi Wabarakatuh
Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam

 

DAFTAR PUSTAKA 

Admin. (n.d.). Menentukan Determinan Matriks Berordo 2x2 dan 3x3 . Retrieved September 7, 2020, from www.madematika.net: https://www.madematika.net/2015/08/menentukan-determinan-matriks-berordo.html

Admin. (n.d.). Soal Dan Pembahasan Kesamaan Matriks. Retrieved September 7, 2020, from mataseluruhdunia208.blogspot.com: https://mataseluruhdunia208.blogspot.com/2018/06/soal-dan-pembahasan-kesamaan-matriks.html

Ammariah, H. (2019, 7 Desember). Matematika Kelas 11 | Cara Mencari Determinan dan Invers Matriks. Retrieved September 7, 2020, from blog.ruangguru.com: https://blog.ruangguru.com/cara-mencari-determinan-dan-invers-matriks

Baru, G. (2020, Mei 5). Invers Matriks. Retrieved September 7, 2020, from rumusrumus.com: https://rumusrumus.com/invers-matriks/

Isetiabhakti. (2019, Oktober 10). Mencari Determinan Matriks (3×3) Dengan Metode Ekspansi Kofaktor. Retrieved Sepember 7, 2020, from medium.com: https://medium.com/@isetiabhakti/mencari-determinan-matriks-3-3-dengan-metode-ekspansi-kofaktor-cad6afd0f57d

Pintar, K. (2020, Juni 20). Cara Mencari Determinan Matriks yang Mudah. Retrieved September 7, 2020, from www.kelaspintar.id: https://www.kelaspintar.id/blog/tips-pintar/cara-mencari-determinan-matriks-yang-mudah-5484/

Rahmah, A. (2020, Januari 18). Determinan Matriks Ordo 2×2 3×3 nxn dan Contoh Soalnya. Retrieved September 7, 2020, from rumus.co.id: https://rumus.co.id/determinan-matriks/