Paisal Vieri Eka Tama Simbolon (28) XI IPS 2
Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
ﺇِﻥَّ
ﺍﻟْﺤَﻤْﺪَ ﻟِﻠَّﻪِ ﻧَﺤْﻤَﺪُﻩُ ﻭَﻧَﺴْﺘَﻌِﻴْﻨُﻪُ ﻭَﻧَﺴْﺘَﻐْﻔِﺮُﻩْ
ﻭَﻧَﻌُﻮﺫُ ﺑِﺎﻟﻠﻪِ ﻣِﻦْ ﺷُﺮُﻭْﺭِ ﺃَﻧْﻔُﺴِﻨَﺎ ﻭَﻣِﻦْ ﺳَﻴِّﺌَﺎﺕِ
ﺃَﻋْﻤَﺎﻟِﻨَﺎ، ﻣَﻦْ ﻳَﻬْﺪِﻩِ ﺍﻟﻠﻪُ ﻓَﻼَ ﻣُﻀِﻞَّ ﻟَﻪُ ﻭَﻣَﻦْ ﻳُﻀْﻠِﻞْ ﻓَﻼَ
ﻫَﺎﺩِﻱَ ﻟَﻪُ. ﺃَﺷْﻬَﺪُ ﺃَﻥَّ ﻻَ ﺇِﻟَﻪَ ﺇِﻻَّ ﺍﻟﻠﻪ ﻭَﺃَﺷْﻬَﺪُ ﺃَﻥَّ
ﻣُﺤَﻤَّﺪًﺍ ﻋَﺒْﺪُﻩُ ﻭَﺭَﺳُﻮْﻟُﻪُ.
Saya
akan memperkenalkan diri. Saya Paisal Vieri Eka Tama Simbolon (28)
murid kelas XI IPS 2 di Sekolah Menengah Atas Negeri 63 Jakarta.
Daerah Istimewa Yogyakarta Source : Google.com
SOAL KONTEKSTUAL YANG BERHUBUNGAN DENGAN TURUNAN
Contoh Soal :
Contoh Soal 1
Kawat sepanjang 120 m akan dibuat kerangka seperti pada gambar dibawah
ini. Agar luasnya maksimum panjang kerangka (p) tersebut adalah...
A. 16 m
B. 18 m
C. 20 m
D. 22 m
E. 24 m
Pembahasan :
Persamaan kerangka :
3p + 4l = 120
4l = 120 − 3p
l = 30 − 34
p
Persamaan luas :
L = p × 2
l
L = p × 2 (30 −
34p)
L = 60p − 32
p2
Luas akan maksimum jika :
L' = 0
60 − 3p = 0
⇒
p = 20
Jadi, panjang kerangka agar luas maksimum adalah 20 m.
Jawaban : C
Contoh Soal 2
Suatu perusahaan menghasilkan produk yang dapat diselesaikan dalam x jam dengan biaya per jam (4x−800+120x) ratus ribu rupiah. Agar biaya minimum, produk tersebut dapat diselesaikan dalam waktu...
A. 40 jam
B. 60 jam
C. 100 jam
D. 120 jam
E. 150 jam
Pembahasan :
Biaya per jam : 4x − 800 + 120x
Biaya untuk x jam :
B(x) = (4x − 800 + 120x)x
B(x) = 4x2 − 800x + 120
Biaya akan minimum jika :
B'(x) = 0
8x − 800 = 0
⇒ x = 100
Jadi, waktu yang diperlukan agar biaya minimum adalah 100 jam.
Jawaban : C
Contoh Soal 3
Selembar karton berbentuk persegi panjang dengan lebar 5 dm dan panjang 8
dm akan dibuat kotak tanpa tutup. Pada keempat pojok karton dipotong
persegi yang sisinya x dm. Ukuran kotak tersebut (panjang, lebar,
tinggi) agar volume maksimum berturut-turut adalah...
A. 10 dm, 7 dm, 1 dm
B. 8 dm , 5 dm, 1 dm
C. 7 dm, 4 dm, 2 dm
D. 7 dm, 4 dm, 1 dm
E. 6 dm, 3 dm, 1 dm
Pembahasan :
Ukuran balok :
p = 8 − 2x
l = 5 − 2x
t = x
V = p
lt
V = (8 − 2x)(5 − 2x) x
V = (40 − 26x + 4x
2) x
V = 4x
3 − 26x
2 + 40x
Volume akan maksimum jika :
V' = 0
12x
2 − 52x + 40 = 0
3x
2 − 13x + 10 = 0
(3x − 10)(x − 1) = 0
x =
103 atau x = 1
Untuk x = 1, maka
p = 8 − 2x = 8 − 2(1) =
6
l = 5 − 2x = 5 − 2(1) =
3
t = x =
1
Jadi, volume akan maksimum jika panjang, lebar dan tinggi balok berturut-turut 6 dm, 3 dm, 1 dm.
Jawaban : E
Contoh Soal 4
Suatu perusahaan menghasilkan x produk dengan biaya sebesar (9.000+1.000x+10x2)
rupiah. Jika semua hasil produk perusahaan tersebut habis dijual dengan
harga Rp5.000,00 untuk satu produknya, maka laba maksimum yang dapat
diperoleh perusahan tersebut adalah...
A. Rp149.000,00
B. Rp249.000,00
C. Rp391.000,00
D. Rp609.000,00
E. Rp757.000,00
Pembahasan ;
Biaya produksi x produk : 9.000 + 1.000x + 10x2
Biaya penjualan x produk : 5.000x
Laba = Biaya penjualan − Biaya produksi
L(x) = 5.000x − (9.000 + 1.000x + 10x2)
L(x) = 5.000x − 9.000 − 1.000x − 10x2
L(x) = −10x2 + 4.000x − 9.000
Laba akan maksimum, jika :
L'(x) = 0
−20x + 4.000 = 0
⇒ x = 200
Jadi, laba akan maksimum jika perusahaan menghasilkan 200 produk, dengan laba maksimumnya adalah :
L(200) = −10(200)2 + 4.000(200) − 9.000
L(200) = −400.000 + 800.000 − 9.000
L(200) = 391.000
Jawaban : C
Contoh Soal 5
Suatu perusahaan memproduksi x unit barang dengan biaya (5x2−10x+30)
dalam ribuan rupiah untuk tiap unit. Jika barang tersebut terjual habis
dengan harga Rp 50.000,00 tiap unit, maka keuntungan maksimum yang
diperoleh perusahaan tersebut adalah...
A. Rp10.000,00
B. Rp20.000,00
C. Rp30.000,00
D. Rp40.000,00
E. Rp50.000,00
Pembahasan :
Biaya produksi x unit : (5x2 − 10x + 30)x
Biaya penjualan x unit : 50x
(kedua biaya diatas dalam ribuan rupiah)
Keuntungan = Biaya penjualan − Biaya produksi
U(x) = 50x − (5x2 − 10x + 30)x
U(x) = 50x − 5x3 + 10x2 − 30x
U(x) = −5x3 + 10x2 + 20x
Keuntungan akan maksimum jika :
U'(x) = 0
−15x2 + 20x + 20 = 0 (bagi −5)
3x2 − 4x − 4 = 0
(3x + 2)(x − 2) = 0
x = 32 atau x = 2
Jadi, keuntungan akan maksimum jika perusahaan memproduksi 2 unit barang, dengan keuntungan maksimumnya adalah :
U(2) = −5(2)3 + 10(2)2 + 20(2)
U(2) = −40 + 40 + 40
U(2) = 40 (dalam ribuan rupiah)
Jawaban : D
Contoh Soal 6
Untuk memproduksi x unit pakaian dalam satu hari diperlukan biaya produksi (x2+4x−10) ratus ribu rupiah. Harga jual pakaian itu tiap unitnya adalah (20−x) ratus ribu rupiah. Keuntungan maksimum yang dapat diperoleh setiap harinya adalah ⋯⋅
A. Rp1.200.000,00 D. Rp2.000.000,00
B. Rp1.500.000,00 E. Rp2.200.000,00
C. Rp1.800.000,00
) dianggap sebagai fungsi terhadap variabel x (ingat bahwa keuntungan didapat dengan mengurangi harga jual terhadap pengeluaran/biaya produksi), sehingga
U(x)=x(20−x)−(x2+4x+10)=20x−x2−x2−4x+10=−2x2+16x−10
Keuntungan akan maksimum apabila U′(x)=0
U′(x)=0−4x+16=04x=16x=4
Keuntungan maksimum tercapai saat memproduksi 4 unit pakaian, yaitu
U(4)=−2(4)2+16(4)−10=−32+64−10=22
Jadi, keuntungan maksimum yang dapat diperoleh setiap harinya adalah Rp2.200.000,00.
(Jawaban E) Contoh Soal 7
Dari kawat yang panjangnya 500 meter akan dibuat kerangka balok yang salah satu rusuknya 25 meter. Jika volume baloknya maksimum, maka panjang dua rusuk lainnya adalah ⋯ meter.
A. 10 dan 90 D. 40 dan 60
B. 15 dan 85 E. 50 dan 50
C. 25 dan 75
Nyatakan l (lebar balok) dalam t (tinggi balok) dengan menggunakan keliling balok (k) tersebut.
k=5004(p+l+t)=50025+l+t=125l+t=100l=100−t
Nyatakan volume tabung (V) sebagai fungsi terhadap variabel t.
V(t)=p×l×t=25×(100−t)×t=2.500t−25t2
Volume balok akan maksimum saat V′(t)=0, sehingga ditulis
V′(t)=02.500−50t=050t=2.500t=50
Untuk t=50, maka l=100−50=50.
Jadi, panjang dua rusuk lainnya adalah 50 meter.
(Jawaban E)
Contoh Soal 8
Sebuah taman berbentuk persegi panjang dengan keliling (2x+24) meter dan lebar (8−x) meter. Agar luas taman maksimum, panjang taman tersebut adalah ⋯ meter.
A. 4 C. 10 E. 13
B. 8 D. 12
Pembahasan
Panjang taman tersebut dapat ditentukan dengan menggunakan keliling dan lebarnya.
k=2(p+l)2x+24=2(p+8−x)x+12=p+8−xp=2x+4
Nyatakan luas persegi panjang sebagai fungsi terhadap variabel x.
L(x)=p×l=(2x+4)(8−x)=−2x2+12x+32
Luas akan maksimum saat L′(x)=0, sehingga
L′(x)=0−4x+12=04x=12x=3
Saat x=3, diperoleh
p=2x+4p=2(3)+4=10
Jadi, panjang taman tersebut adalah 10 meter
(Jawaban C)
Contoh Soal 9
Sebuah taman berbentuk persegi dengan keliling (2x+24) m dan lebar (8−x). Agar luas taman maksimum, maka panjang taman tersebut adalah...
A. 4 m
B. 8 m
C. 10 m
D. 12 m
E. 13 m
Pembahasan :
K = 2x + 24 = 2(x + 12)
l = 8 − x
K = 2(p + l)
2(x + 12) = 2(p + 8 − x)
x + 12 = p + 8 − x
p = 2x + 4
L = p . l
L = (2x + 4)(8 − x)
L = −2x2 + 12x + 32
Luas akan maksimum jika :
L' = 0
−4x + 12 = 0
⇒ x = 3
p = 2x + 4
p = 2(3) + 4
p = 10
Jadi, panjang taman agar luas maksimum adalah 10 m.
Jawaban : C
Contoh Soal 10
Dua bilangan m dan n memenuhi hubungan 2m − n = 40. Nilai minimum dari p=m2+n2 adalah...
A. 320
B. 295
C. 280
D. 260
E. 200
Pembahasan :
2m − n = 40
n = 2m − 40
p = m2 + n2
p = m2 + (2m − 40)2
p = m2 + 4m2 − 160m + 1600
p = 5m2 − 160m + 1600
p akan minimum jika :
p' = 0
10m − 160 = 0
⇒ m = 16
n = 2m − 40
n = 2(16) − 40
⇒ n = −8
p = m2 + n2
p = 162 + (−8)2
p = 320
Jawaban : A
Contoh Soal 11
Icha akan meniup balon karet berbentuk bola. Ia menggunakan pompa untuk
memasukkan udara dengan laju pertambahan volume udara 40 cm2/detik. Jika laju pertambahan jari-jari bola 20 cm/detik, jari-jari bola setelah ditiup adalah...
A. 1√π cm
B. 1√2π cm
C. 12√π cm
D. 23√π cm
E. π cm
Pembahasan :
Laju pertambahan volume udara :
dVdt = 40
Laju pertambahan jari-jari bola :
drdt = 20
Volume bola :
V = 43πr3
dVdr = 4πr2
Dengan aturan rantai :
dVdt = dVdr × drdt
40 = 4πr2 × 20
1 = 2πr2
r2 = 12π
r =
√12π
r =
1√2π
Jawaban : BContoh Soal 12
Sebidang tanah akan dibatasi oleh pagar dengan menggunakan kawat berduri
seperti pada gambar. Batas tanah yang dibatasi pagar adalah yang tidak
bertembok. Kawat yang tersedia 800 meter. Berapakah luas maksimum yang
dapat dibatasi oleh pagar yang tersedia?
A. 80.000 m2
B. 40.000 m2
C. 20.000 m2
D. 5.000 m2
E. 2.000 m2
Pembahasan :
Misalkan panjang area tanah p dan lebar l
Area tanah yang akan dibatasi pagar adalah (p + 2l)
Perhatikan bentuk pagar, karena kawat yang digunakan 4 baris maka
4(p + 2l) = 800
p + 2l = 200
p = 200 − 2l
L = p × l
L = (200 − 2l) × l
L = 200l − 2l2
Luas akan maksimum jika :
L' = 0
200 − 4
l = 0
⇒
l = 50
p = 200 − 2
l
p = 200 − 2(50)
⇒
p = 100
L =
p ×
l
L = 100 × 50
L = 5000
Jadi luas maksimum adalah 5000 m
2
Jawaban : D
Contoh Soal 13
Seorang petani mempunyai kawat sepanjang 80 meter yang direncanakan
untuk memagari kandang berbentuk tiga buah persegi panjang berdempet
yang identik seperti diperlihatkan pada gambar berikut (Sisi di
sepanjang gudang tidak memerlukan kawat). Luas maksimum kandang adalah
...
A. 360 m2
B. 400 m2
C. 420 m2
D. 450 m2
E. 480 m2
Pembahasan :
Misalkan panjang kandang p dan lebar kandang l.
Persamaan panjang kawat yang digunakan untuk memagari kandang :
p + 4l = 80 → p = 80 - 4l
Persamaan luas kandang :
L = pl
L = (80 - 4l)l
L = 80l - 4l2
Turunan pertama L terhadap l :
L' = 80 - 8l
Luas akan maksimum jika L' = 0
80 - 8l = 0
80 = 8l
l = 10
Jadi, luas akan maksimum jika l = 10, dengan luas maksimumnya adalah
L = 80(10) - 4(10)2
L = 800 - 400
L = 400
Jawaban : B
Contoh Soal 14
Sebuah tabung tanpa tutup yang terbuat dari lempengan tipis dapat memuat air sebanyak 27π cm2. Luas permukaan tabung akan minimum jika jari-jari tabung sama dengan ...
A. 9 cm
B. 8 cm
C. 6 cm
D. 4 cm
E. 3 cm
Pembahasan :
Persamaan volume tabung :
V = πr2 t
27π = πr2 t
27 = r2 t
t = 27r2
Persamaan luas tabung tanpa tutup :
L = πr2 + 2πrt
L = πr2 + 2πr(27r2)
L = πr2 + 54πr
Turunan pertama L terhadap r :
L' =
2πr - 54πr2
Luas akan minimum jika L' = 0
2πr - 54πr2 = 0 (kali r2)
2πr3 - 54π = 0
2πr3 = 54π
r3 = 27
⇒ r = 3
Jawaban : E
Contoh Soal 15
Sebuah akuarium tanpa tutup memiliki alas berbentuk persegi panjang
dengan perbandingan panjang dan lebarnya 2 : 3. Jika luas permukaan
akuarium adalah 1.800 cm2, volume maksimum akuarium tersebut adalah ...
A. 3.600 cm3
B. 5.400 cm3
C. 6.300 cm3
D. 7.200 cm3
E. 8.100 cm3
Pembahasan :
pl = 23→ p = 23l
Persamaan luas akuarium tanpa tutup :
pl + 2pt + 2lt = 1.800
(23l)l + 2(23l)t + 2lt = 1.800 (kali 3)
2l2 + 4lt + 6lt = 5400
2l2 + 10lt = 5400
10lt = 5400 - 2l2
t = 540l - 15l
Persamaan volume akuarium :
V = plt
V = 23l . l . (540l - 15l)
V = 360l - 215l3
Turunan pertama V terhadap l :
V' = 360 - 615l2
Volume akan maksimum jika V' = 0
360 - 615l2 = 0
360 = 615l2
l2 = 900
l = 30
Jadi, volume maksimum aquarium adalah
V = 360(30) - 215(30)3
V = 10.800 - 3.600
V = 7.200
Jawaban : D
Terima kasih kepada Ibu DR Lizza Novrida, semoga apa yang pelajari
hari memberikan manfaat dikemudian hari
dan diberkati tuhan yang maha esa.
Wassalamualaikum Warahmatullahi Wabarakatuh
Shalom
Om Swastiastu
Namo Buddhaya
Rahayu
Salam Kebajikan
Salam Sejahtera Untuk Seluruh Alam
DAFTAR PUSTAKA
Maker, Z. (2016, Oktober 2016). Pembahasan Soal UN
Aplikasi Turunan. Retrieved from smatika.blogspot.com:
https://smatika.blogspot.com/2016/10/pembahasan-soal-ujian-nasional-aplikasi.html
S.Pd, S. (2019, Maret 5). Soal dan Pembahasan –
Aplikasi Turunan (Diferensial). Retrieved from mathcyber1997.com:
https://mathcyber1997.com/soal-dan-pembahasan-aplikasi-turunan-diferensial/
![]() , seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan) dan dibaca �integral�.
, seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan) dan dibaca �integral�.![]() f(x) dx disebut integral tak tentu dari f(x). Jika F(x) anti turunan dari f(x), maka
f(x) dx disebut integral tak tentu dari f(x). Jika F(x) anti turunan dari f(x), maka : notasi integral (yang diperkenalkan oleh Leibniz, seorang matematikawan Jerman)


![]() maka
maka ![]() atau dapat dituliskan
atau dapat dituliskan ![]()
![]() f(xdx) = 2x2 + c.
f(xdx) = 2x2 + c. ![]() dengan c suatu konstanta.
dengan c suatu konstanta. ![]()
![]()
![]()
![]()

![]()

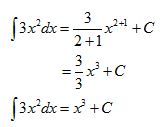
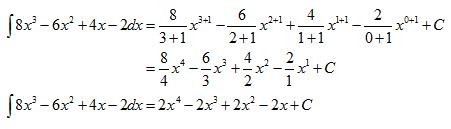
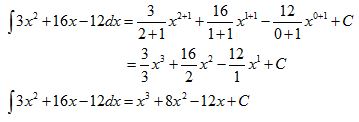

.png)












